I. SCIENCE AND ITS ORIGINS

What is science?

Several views:

1) Behavior by which we gain control over the environment

2) Distinguish between

a) Science - Theoretical knowledge

b) Technology - Practical applications

This view needs more criteria to distinguish scientific from non-scientific theories. For this, see the following views.

3) Scientific theories defined by the form of their statements:

universal, lawlike statements, preferably equations. Ex.: Ideal gas law. Newton's 2^nd law.

4) Define science by its method.

5) Define science by its epistemological status, what kind of justification its claims have.

6) Define science by its content.

7) Procedures or beliefs that are rigorous, precise, objective.

8) "Science" as a term of approval.

"Science" has several legitimate meanings.

'Science' has changed significantly over the centuries. Consequently the historian needs a very broad definition of "science" in order to properly understand the history of science.

"Natural philosophy" and "philosophy of nature":

Narrower than "scientia" and "episteme": Refers to the investigation of nature

Remember Isaac Newton's Mathematical Principles of Natural Philosophy. "Natural philosophy" later came to be called "natural science." Natural philosophy was viewed as a part of the larger quest to understand reality in general.

Prehistoric attitudes toward nature

Knowledge about nature has long been important to our survival.

But distinguish know-how from theoretical knowledge.

People can have practical rules of thumb without knowing the theoretical principles underlying them.

Primitive people transmitted knowledge orally, without writing. Characteristics of oral traditions:

They are fluid (changeable).

Cannot have historical archives or scientific reports.

Function is to justify current social structure and practices.

Primitive people have a different conception of explanations:

They anthropomorphize nature.

They seek individual causes, not causal generalizations.

They explain general features of the world in terms of more familiar processes.

Ex.: African myth about the earth being a mat that has been unrolled and remains tilted, thus explaining upstream and downstream.

Note: What is wrong with this explanation (aside from being generally false)?

General features of primitive world-view:

World divided into earth, sky, and sometimes underworld.

Deities are everywhere. No clear distinctions between human, nature, and supernature.

Belief in ghosts, spirits, and often in reincarnation

Magical rituals for controlling invisible powers.

Parochial conception of space & time.

Ex.: Cardinal directions as "upstream" & "downstream"

An African tribe, the Tio, cannot locate anybody farther than 2 generations in the past.

The present order is explained by its historical origins. History conceived as a series of isolated, decisive events.

Ex.: The story of the 9 Woots:

1. the ocean

2. the digger, who made riverbeds & hills

3. the flowing, who made rivers flow

4. who created the woods and savannas.

5. who created leaves

6. who created stones

7. the sculptor, who made people out of wooden balls

8. the inventor of prickly things

9. the sharpener, who made pointed things

Notice features of this 'explanation':

Anthropomorphization; everything explained by agents

Magical explanations. "Made people out of wooden balls"

Explanations of general features of the world are given in terms of individual, historical events.

The lack of system, lack of attempt at deeper explanations, and lack of ties to empirical evidence.

Human inventions attributed to deities.

Deities identified with physical objects like the ocean. Did they really think the ocean was a person? Cf. the Egyptian myth in which air and moisture give birth to earth and sky. Did they really think that air could have sex with moisture, that one of them could get pregnant, and that earth could come out of it like a baby?! Note the general lack of logic.

The healing arts connected with religion & magic. Witch doctors had both ordinary remedies & magical rituals for driving out spirits.

Primitive people have a different, or no conception of truth (?). Our criteria of truth:

Internal coherence

Correspondence with external reality

Their criterion:

"sanctioned belief". Community consensus.

How did the new conception of knowledge and truth originate:

Stages in the development of writing:

Pictograms: symbols stand for things

Logograms: Symbols stand for important words

Syllabic writing: symbols stand for syllables

Alphabetic writing: symbols stand for individual phonemes

Effects of the development of writing:

Puts stories into a permanent, visible form. Hence, makes possible inspection & comparison between different accounts.

This encourages criticism & the distinction between truth and myth or legend.

Enables people to make detailed lists, inventories.

This makes it possible to discover patterns in the information.

Writing thus led to the beginnings of science & philosophy.

( Other factors: The Greeks had contact with other cultures, including Egypt, the far East, the rest of Europe. This leads to a questioning, philosophical spirit.)

The beginnings of science in Egypt and Mesopotamia

Egyptian mathematics (circa 3000 B.C.):

Egyptians had a decimal number system.

They had geometrical formulae for calculating areas of simple figures and volumes of simple solids (e.g., triangle, rectangle, circle, pyramid)

They devised a simpler calendar, with 12 months of 30 days, plus 5 days at the end.

Mesopotamian mathematics (circa 2000 b.c.):

(Mesopotamia is the site of ancient Babylon & Assyria.)

Used a decimal and sexagesimal number system. Placement of symbols used to indicate powers of 60 (similar to our system, where placement indicates powers of 10).

Notice how this system differs from, say Roman numerals. Notice that this system enables one to write indefinitely large numbers with a limited number of symbols.

They also had generalized fractions.

They had techniques for solving what we would call algebra problems, e.g., given x*y and x+y, determine the values of x and y.

Babylonian astronomy:

Mapped some of the heavens, including prominent stars & constellations

Noted two kinds of celestial bodies: (a) the fixed stars, (b) the wandering stars, or planets (incl. sun & moon).

Identified the zodiac & divided it into 12 equal segments. The planets move through the zodiac.

Babylonian astronomers could predict motions of the planets, eclipses, and the appearance of the new moon.

Astronomy was also connected with astrology: the attempt to make predictions about human affairs, on the basis of the motions of the planets.

Egyptian & Mesopotamian medicine: it had 3 elements:

a) They believed diseases were caused by evil spirits. They had magical rituals for driving out the spirits

b) They also had medicines, and

c) They practiced surgery.

Note the beginnings of science. Their medical doctrine (though primitive) included careful observations of symptoms & cataloguing of ailments.

The world of Homer and Hesiod

The ancient Greeks credited Homer with writing:

The Iliad: The story of the Trojan War.

The Odyssey: The story of Odysseus' journey home after the Trojan War.

Hesiod wrote the Theogony: an account of the origin of the world and the gods. It describes the genealogy of the gods, and the major conflicts they underwent. Includes the overthrow of Kronos & the Titans by Zeus & the gods. Greek gods, together with their functions, include:

Zeus (the sky, weather, lightning, law & morality)

Hera (weddings & marriage; Zeus' wife)

Athena (war, protector of cities, wisdom)

Hades (underworld, the dead)

Ares (war)

Poseidon (the ocean, storms, earthquakes)

The gods are portrayed as taking an active role in human affairs. Nature was unpredictable, due to the possibility of divine whims.

Did people really believe these incredible, often nonsensical stories?

Compare: When people pray to God, thank God, do they really think God is intervening in their lives? In what way? Ex.:

An athlete asking God for a victory

Thanking God for your food at the dinner table

The first Greek philosophers

The first Greek philosophers (pre-Socratic) include: Thales, Pythagoras, Heraclitus, Anaximander.

Philosophy arose alongside mythology. But philosophy had distinguishing characteristics:

An attempt to understand nature rationally. Emphasis on argumentation.

Explanations appeal to the natures of things, not divine intervention. Explanations are sought in physical causes, rather than the motives of the gods.

Hence, nature is regarded as predictable, orderly, not capricious.

Note that this is the beginning of a scientific conception of causality.

The Milesians & the question of ultimate reality

The Milesians were a group of pre-Socratic philosophers from Miletus (in Ionia).

They held

materialism: the world is composed of physical material

monism: there is basically only one kind of stuff

Thales, famously, held that everything is composed of water.

The atomists (Leucippus, Democritus):

Everything is made of atoms (tiny, indivisible particles), moving around in the void. Their different configurations account for the differences in observed substances.

The theory of the 4 elements became popular later. The elements were earth, air, fire, and water.

Pythagoreans: followers of Pythagoras, who held that numbers were the most important, fundamental reality.

The problem of change

Heraclitus claimed that everything is constantly changing. It is impossible to step into the same river twice.

Parmenides argued that change is impossible. Why?

There are only two possible kinds of change: (a) being passing into non-being, (b) non-being passing into being.

Non-being can't exist (for then it would be being).

Therefore, (a) is impossible, for it would require non-being to exist at the later time.

Similarly, (b) is impossible.

Zeno says: Motion is impossible. 2 of Zeno's paradoxes:

(I) Imagine that you wanted to walk from point A to point B. In order to do so, you must first go ½ the distance. Then, you must go ½ the remaining distance (3/4 of the total distance), then ½ the remaining distance again, and so on. So:

1. In order to get to point B, you must complete the series (1/2, 3/4, 7/8, ...).

2. (1/2, 3/4, 7/8, ...) is an infinite series, which means it has no end.

3. An infinite series cannot be completed (for it has no end).

4. Therefore, you cannot complete the series (1/2, 3/4, 7/8, ...).

5. Therefore, you cannot get to point B.

(II) The race between Achilles and the tortoise. The tortoise gets a head start, but Achilles (assume) runs faster. When Achilles gets to the point where the tortoise started (point A), the tortoise has moved ahead a little bit (to point B). When Achilles gets to B, the tortoise has again moved ahead a little (to point C). Etc. Thus, Achilles must complete an infinite series in order to catch up to the tortoise. Therefore, he cannot catch up to the tortoise.

What about observations of motion, change??

Parmenides, Zeno say that the senses cannot be trusted. Change is only an illusion. We should trust reason over the senses.

The problem of knowledge

Parmenides & Zeno demonstrate epistemological concerns:

a) The attempt to provide an objective reason for one's conclusions. Notice how this differs from earlier, primitive thought.

b) The distinction between appearance and reality. The idea that things might be radically different from the way they appear.

c) The contrast between reason and the senses, and the preference given to the former.

Plato's world of forms

Relationship between Socrates & Plato: Plato was a student of Socrates. Plato wrote many dialogues in which Socrates figures.

Socrates died in 399 b.c. (executed, famously)

Plato divided reality into two realms:

a) The material world, concrete objects: perceived by the senses, changing, imperfect, somehow 'less real'. Like imitations of the Forms.

b) The Forms: Grasped by the intellect, unchanging, perfect, more real (whatever that means).

Arguments for the forms:

The 'one over many' argument: some classes of concrete objects have something in common. Like redness, beauty, tablehood. What is this 'something'? A Form (modern philosophical terminology: a "universal").

The imperfection of the material world: there are no (perfect) circles in the material world, but yet we have an idea of a (perfect) circle. What can this idea represent? The Form of circularity.

The allegory of the cave illustrates this doctrine.

Important epistemological points:

a) Again, Plato places intellect above the senses.

b) More importantly: he recognizes that what is important is what is universal, not what is particular. Compare this to modern science, which seeks explanations in terms of universal laws, and contrast with pre-scientific thinking. Scientists study universals (contrast history, which studies particular events).

Plato's cosmology

The world was created by a divine being, the Demiurge.

The Demiurge works with pre-existing materials with their own limitations

He acts according to a rational plan. This explains the order in the world.

The 5 regular solids are associated with elements:

Tetrahedron (4) -- Fire

Cube (6) -- Earth

Octahedron (8) -- Air

Dodecahedron (12) -- the cosmos as a whole (?)

Icosahedron (20) -- Water

Each element is composed of geometrical shapes.

Elements (except earth) can be transmuted by the recombination of their component triangles.

All observable substances are made of varying amounts of these 4 elements.

The world as a whole is a living thing, with a body and soul. The soul is responsible for all motion in the cosmos.

What Plato knew about the heavenly bodies. Different things you can see in the sky:

The fixed stars (almost all of the stars): these retain the same positions relative to each other. They're on a sphere (centering on the earth), rotating around the earth once a day.

The wandering stars (planets): Like the fixed stars, but they move relative to the fixed stars and each other. They always stay within a certain band of sky, though (the zodiac)

The sun: it moves in a certain band of sky (narrower than the zodiac, I think), called the ecliptic.

[Real reason: because the earth's axis of rotation is tilted.]

The achievement of early Greek philosophy

The ancient Greek philosopher/scientists discussed some of the same questions we investigate today (e.g., where did the world come from, what are the ultimate constituents of material objects, how is the cosmos arranged).

Other questions are largely forgotten, or relegated to 'philosophy' (how is change possible, how to balance reason vs. observation, how real are universals and particulars).

The latter are foundational questions, which they had to begin with. The Greeks laid the foundations for future investigation of nature, which we today take for granted.

[Is that really true? Exactly what are these foundations?]

Life and Works

Important life events:

Lived 384-322 B.C. (62 years) So he was young when Socrates died.

Studied with Plato for 20 years.

Tutored Alexander the Great.

Works:

Wrote major treatises on many areas of science & philosophy, including: logic, metaphysics, ethics, politics, aesthetics, physics, biology, and cosmology. Founded the science of logic.

Alas, most of his work has been lost.

Metaphysics & Epistemology

Rejects Plato's theory of Forms:

Particular things have independent reality.

Immanent realism: Universals exist only in particular things.

Matter & form always coexist in particular things:

Form: roughly, the collection of properties a thing has.

Matter: the substance (ultimate subject) which has those properties.

Holds an empiricist epistemology: All knowledge derives from experience.

1. First stage is sensory experiences.

2. Repeated experience yields memory.

3. By induction, one comes to grasp the essences of things, or universal definitions.

4. Scientific understanding is then completed when we see how to deduce particular aspects of observed things from their essences.

Did Aristotle employ this method in practice? Probably not.

[That's odd, isn't it? Couldn't he have observed himself in order to see how scientific thought actually proceeds?]

Nature & Change

In all change, there is something constant:

The matter remains

but it changes its form

Change is always between contraries (e.g. from hot to cold, or vice versa). It is between a form and its absence ('privation').

An answer to the Parmenidean challenge: Change is not merely a passing from non-being into being. Instead, there are 3 things:

a) Non-being

b) Potential being

c) Actual being.

Change is a transition from potentiality to actuality.

What causes change? The 'natures' of things. About natures:

Living things and the elements have natures. Artefacts do not.

The nature of an organism is not merely a summation of the natures of its constituents.

The nature of a thing is sort of like an inherent striving towards some end. Ex.: the element Earth has a natural place, which happens to be the center of the cosmos. That is why, if lifted away from that place, it strives to move back towards the center.

[Moliere made fun of this aspect of Aristotle's philosophy in his (Moliere's) play Le Malade Imaginaire. Asked why opium puts people to sleep, the Aristotelian doctor answers, "Because it possesses a virtus dormitiva" (Latin for "sleep-inducing power").]

The 4 causes:

Formal cause

Material cause

Efficient cause

Final cause

Aristotle's theory of nature is teleological: things behave in the way they do because of the end state they are innately tending towards. This idea is sort of taken up in modern biology, where one frequently hears about the functions of things.

[Things have functions or purposes. Note that this is not a psychological concept. Inanimate objects have functions according to Aristotle, which are inherent in their natures.]

Why Aristotle did not use controlled experiments: he thought that the nature of a thing would only be manifested in its natural circumstances. Artificial situations distort our evidence.

Cosmology

The elements: Earth, Air, Fire, & Water, plus a fifth element ("quintessence"), the aether. All other substances are mixtures of the first 4.

Fundamental properties: hot/cold, wet/dry

Earth: Cold & dry

Air: Hot & wet

Water: Cold & wet

Fire: Hot & dry

'Levity' of the elements (the contrary of weight) determine their natural positions. In order from heaviest to lightest:

Earth, Water, Air, Fire, Aether.

Heaviest elements tend towards the center of the cosmos; light elements towards the periphery.

Notice how this scheme explains: Earth sinks in water, so is heavier than it; air rises above water, so is lighter than it; Fire (flames) point upward, because fire is lighter than air.

Explains why the earth is spherical and at the center of the universe, and why it is surrounded by air.

The earth is surrounded by a concentric, spherical shell, the lunar sphere, which the moon is on, orbiting the earth. This divides the universe into 2 regions:

The terrestrial (sublunar) region, the region below the lunar shell: subject to generation, corruption [the contrary of generation].

The celestial region, that beyond the lunar shell: contains stars in unchanging patters of motion, amidst the aether. The celestial region is essentially changeless, uncorruptible.

The universe is a plenum (nature abhors a vacuum): all space is occupied.

That the ancients and medievals thought the Earth was flat is just a myth. Aristotle estimated the Earth's circumference, at about 1.8x the modern value. (De Caelo II.13) This may be the oldest recorded estimate.

Motion, Terrestrial & Celestial

All motion divides into 2 kinds:

Natural -- caused by a thing's nature

Forced -- caused by an external force (another object)

Motion is positively correlated with the motive force & inversely related to the resistance (thinner media resist less).

[Note: Forces are required to move things, not to change their state of motion as in Newton.]

Falling objects: speed is proportional to their weight (controlling for resistance).

Objection: Why do thrown objects continue in that direction after they leave your hand?

A: The medium (air) helps push them along.

[Notice that, at a first glance, this theory of motion corresponds to observation, and Newton's theory does not.]

Celestial motions:

The celestial sphere rotates around the earth once/day.

The fixed stars are fixed to the celestial sphere.

The sun moves on the celestial sphere around the ecliptic, once per year. Thus, it has its circular motion around the ecliptic superimposed on the daily rotation of the celestial sphere itself.

The moon moves on the same path, but making the circuit once per month.

Other planets have similar motions, but with occasional reverses.

[This is an elaborate system, accounting for the observed motions of the celestial bodies. Imagine the task of trying to account for those motions, without the benefit of a modern astronomy textbook. It's far from obvious that another system exists.]

Celestial bodies are moved by 'Prime Movers' or unmoved movers -- divine beings that the celestial objects strive to imitate. [People often refer to "the Prime Mover" in Aristotle, but note that there are more than one. Each body has its own.]

Aristotle as a Biologist

Aristotle collected lots of empirical data. He mentions over 500 different species, often describing them in meticulous detail. Witness his description of the development of chicken eggs. (And think about the observations required to obtain this information.)

The aim of these observations is to understand the causes of things.

Organisms (like everything) consist of matter and form.

Matter is supplied by the female, in reproduction. It is the material the organism is made of, including the various body parts.

Form is supplied by the male. It includes the way the matter is arranged; also includes the organism's final cause, the end towards which it strives. Form = soul: there are 3 kinds of soul:

1) The vegetative soul: responsible for nutrition & growth

2) The animal soul: responsible for perception & self-movement

3) The rational soul: responsible for thinking, reasoning.

Plants, animals, and humans are differentiated by the souls they possess.

[ Note that this is very different from the modern, Christian-inspired concept of "soul".]

Note: The soul is an aspect or attribute of the organism as a whole. Therefore, persistence of the soul after destruction of the body is logically impossible.

In growth, the organism moves from potentiality to actuality. The adult form is the final cause, the full 'actualization' of the organism. Particular events in the development are explained by the end it is aiming at.

Aristotle arranges living things in a hierarchy of superiority:

Prime Mover

humans

viviparous animals (bearing live young)

oviparous animals (egg-laying)

vermiparous animals (bearing larvae)

plants

This is supposedly related to the amount of 'vital heat' in living things. Related point: the lungs function to cool the organism.

[Can you think of empirical ways to test this theory?]

Aristotle's Achievement

[ Aristotle may have been the greatest thinker in history:

He wrote comprehensively, on all manner of subjects.

He put forward plausible theories that seemed to account for the observations, as well as studiously taking into account the opinions and arguments of his predecessors.

He single-handedly founded the science of logic, and wrote major works in many other disciplines.

In most cases, his theories became the accepted theories for centuries to follow.

Moreover, he integrated all of what he knew about the world into a single, coherent system. We see this in his application of the ideas of potentiality/actuality, matter/form, and the 4 causes to the different fields he investigated.

Note that Aristotle relies on arguments & observations, not on tradition or superstition. Also, what he can say at any given point is logically constrained by the rest of his system; unlike earlier, pre-scientific thought, which seems unconcerned about contradictions & arbitrariness.]

IV. HELLENISTIC NATURAL PHILOSOPHY

Hellenistic culture: the culture of the Greek empire established by Alexander -- mainly Greek, but with elements borrowed from the other, conquered territories.

Schools & Education

The Greeks lacked the formal school system we have -- no compulsory education, no state-run schools; education was for the few.

Early education efforts: focused on athletics (gymnastike) and the arts (mousike)

The sophists: introduced intellectual, esp. political education. Trained people to be good citizens & statesmen. They taught in public places, for a fee. (Socrates did not approve of the sophists.)

The Academy: Founded by Plato just outside Athens. People could listen to lectures & discussions at no charge. It became a permanent school. Aristotle studied at the Academy, with Plato.

The Lyceum: School founded by Aristotle after Plato's death [possibly because Aristotle was denied leadership of the Academy]. Started the practice of cooperative research, as in his work on natural history. Followers of Aristotle came to be called "peripatetics" [either after the colonnaded walk they met in, or after Aristotle's habit of walking about while lecturing.]

The Stoa: Another school founded by Zeno of Citium (not to be confused with Zeno of Elea). They met in a covered walkway (a stoa). This led to their being called stoics (leading to the present-day adjective "stoic" or "stoical"). [The stoics favored learning to accept whatever happens in life and freeing oneself of strong passions.]

The Epicurean Garden: Place where Epicurus taught. [He advocated a mild-mannered hedonism & egoism. People should seek the greatest pleasure or satisfaction in life, which will be achieved by learning to be content with the simple pleasures. Led to the present-day adjective "epicurean."]

After Alexander's death the empire is split. [Alexander left his empire, in his own words, "To the strongest."] Ptolemy takes control of Alexandria (in Egypt), which becomes another center of learning, surpassing Athens and including the Museum (a temple to the Muses). This is the first instance of state support of education.

Alexandria was originally founded by Alexander during one of his military campaigns.

It became the site of a famous library, housing almost 500,000 books. The Library of Alexandria, however, was destroyed over several centuries.

The Lyceum after Aristotle

Theophrastus: Friend of Aristotle. Succeeded him as head of the Lyceum after Aristotle's death. Continued Aristotle's investigations of natural history. Also questioned some aspects of Aristotle's theories, including: observed that not everything in nature seems to have a purpose. Composed the definitive work on botany for his time through the middle ages. Left his land to the school upon his death.

Strato: Successor of Theophrastus. Further carried on the Aristotelian program. Important corrections to Aristotle:

Argued that bodies had a range of weights, not just 'heavy' and 'light'.

Air and fire rise, not because of their 'levity', but because they are displaced by heavier bodies. [This is the correct account -- i.e., there is no force internal to light objects pushing them upward; they are merely less pulled downward than the surrounding heavier objects.]

Bodies accelerate as they fall. Evidence:

Falling water makes a continuous stream near the top; discontinuous near the bottom.

The impact of a body is related to the height from which it falls, not just its weight.

[All correct, and astute.]

Strato allowed void spaces, within bodies. (But was not a full-fledged atomist.) This could explain how a body could expand or contract.

Aristotle remains influential until the 500's A.D. Later philosophers comment on and systematize his works.

Epicureans & Stoics

Epicurean doctrines:

Happiness as the end of life. Ethics as the central branch of philosophy.

Atomism & materialism: Everything consists of atoms in the void.

[ Atomism first invented by Democritus.]

No final causes; only mechanistic, efficient causes.

Atoms lack secondary qualities; they have only primary qualities (size, shape, weight)

The atomic swerve: accounts for

a) Why atoms can collide

b) how we can have free will. Note: Epicurus was apparently the first to perceive the conflict between free will and mechanism.

No gods.

Stoic doctrines:

Happiness as the end of life. Ethics as the central branch of philosophy.

Also accepted materialism: Only physical stuff exists.

But matter is not wholly passive. It has an active element, pneuma (breath):

Pneuma is a subtle substance that permeates everything. 3 kinds of pneumas:

1) Hexis: present in inorganic matter. Explains cohesion, by varying amounts of tension. (How could the epicureans explain why objects stick together?)

2) Physis: Present in plants & animals. Explains vital properties.

3) Psyche (soul): Present in humans, explains rationality.

Pneumas occupy the same space as the ordinary, passive matter.

Cosmology: The universe is in an infinite cycle of expansion and contraction.

The universe is purposeful (due to the pneuma existing throughout it), but deterministic (everything has a cause). Cicero's remark: "...This makes it intelligible that fate should be, not the 'fate' of superstition, but that of physics."

The Application of Mathematics to Nature

How important is mathematics to understanding nature?

Plato & Pythagoras -- mathematical objects are the fundamental realities. Pythagoras is said to have thought that everything consists of numbers; Plato thought matter composed of geometric figures.

Aristotle -- Physics and mathematics are distinct, but both useful sciences. They deal with different aspects of natural objects. Mathematicians abstract away from the sensible qualities of bodies, leaving only "quantity and continuity."

[How is this issue resolved in modern thought? No one thinks nature is actually composed of mathematical objects. At the same time, physicists deal mainly with equations, vectors, and other mathematical objects. Learning physics is largely learning to manipulate these mathematical systems.]

Greek Mathematics

Incommensurable quantities:

Greeks discovered the existence of incommensurable lines, which at the time was felt to be strange and paradoxical. They are called 'incommensurable' meaning "incapable of being compared" because, roughly, they have no determinate ratio to each other. Ex.: The diagonal and the side of a square are incommensurable.

Correspond to: Irrational numbers. Called "irrational" because they cannot be stated as a ratio (of whole numbers). 2 is irrational, and so is .

Geometry:

Euclid's Elements from ca. 300 b.c. systematizes geometry. This becomes the definitive work on geometry until the 19^th century.

Important: uses deductive proof starting from definitions and self-evident axioms. This becomes an ideal for scientists, mathematicians and philosophers to strive for, for the rest of history.

The Elements is divided into:

Definitions, including:

A point is that which has no part.

A line is breadthless length.

A straight line is a line which lies evenly with the points on itself.

A surface is that which has length and breadth only.

A plane surface is a surface which lies evenly with the straight lines on itself.

A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.

When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.

Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.

Etc.

Postulates [really, axioms pertaining specifically to geometry]:

1. To draw a straight line from any point to any point.

2. To produce a finite straight line continuously in a straight line.

3. To describe a circle with any center and radius.

4. That all right angles equal one another.

5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. [The famous 'axiom of parallels,' rejected in non-Euclidean geometries]

Axioms, or common notions: [general mathematical axioms not specific to geometry]

1. Things which equal the same thing also equal one another.

2. If equals are added to equals, then the wholes are equal.

3. If equals are subtracted from equals, then the remainders are equal.

4. Things which coincide with one another equal one another.

5. The whole is greater than the part.

Propositions:

A series of theorems proved from the above, and constructions allowed according to the above, which you should have learned about in high school geometry class. Ex.:

The interior angles of any triangle sum to two right angles.

To draw a straight line perpendicular to a given plane from a given elevated point.

The 'propositions' cover plane geometry, solid geometry, and even some of number theory.

Archimedes:

Follows Euclid. More work on plane & solid geometry, arithmetic, & mechanics. Among other things, he was proud of discovering that the volume of a sphere is 2/3 the volume of the cylinder that circumscribes it. It is said that this formula was put on his tombstone. Made a more accurate estimate of : 3 10/70 < < 3 10/71. More on his mechanics later.

Apollonius: work on conic sections.

Early Greek Astronomy

Early astronomy used to set the calender. Problem:

They attempted to account for the lunar cycle and the solar cycle in the calendar (hence months & years). But the lunar cycle does not divide evenly into the solar cycle.

One solution: the Metonic calendar, based on the fact that 19 solar cycles = 235 lunar cycles. Thus, you can have a 19-yr. cycle, with 12 yrs of 12 months + 7 yrs of 13 months. (12×12 + 7×13 = 235.)

[Modern solution: Forget the lunar cycle.]

The 2-sphere model (Plato & Eudoxus): Involves uniform circular motions superimposed on the daily rotation of the 'celestial sphere'.

Every heavenly body circles the celestial sphere once per day. [Modern explanation: the earth's daily rotation.]

But each heavenly body also makes a circuit around the ecliptic, in its own peculiar time period. [Modern explanation: the earth's yearly circuit around the sun]

Important astronomical terms:

Ecliptic: circular path that bodies follow (roughly) around the earth. It is tilted at 23 to the equator of the celestial sphere.

Equinox: time when the ecliptic intersects the equator of the celestial sphere. (Days & nights equally long.) Spring equinox: this happens at the beginning of spring. Fall equinox: at the beginning of fall.

Solstice: Time when the sun is farthest from the equator of the celestial sphere. Summer solstice: This happens in mid-summer (days are longest). Winter solstice: This happens in mid-winter (nights are longest).

An anomaly: Retrograde motions. Periodically, on its path around the ecliptic, a planet reverses direction for a bit. Each planet is on its own cycle for retrograde motions. This only applies to Mercury, Venus, Mars, Jupiter, Saturn; not the sun or moon. [They couldn't see Neptune, Pluto, or Uranus.] [Modern explanation: planets' circuit around the sun.]

Eudoxus' solution: A series of nested, concentric spheres, each tilted with respect to the others, and each rotating uniformly (but not all in the same direction).

This provides a rough, qualitative account for the observable motions of planets.

Eudoxus did not conceive the spheres as physically real; they're just a mathematical device for describing planetary motions, i.e. breaking complex motions into components consisting of uniform circular motions.

Interestingly, Mercury & Venus never stray very far from the sun.

Aristotle took the spheres more seriously, as physically real. He inserted 'counter-acting' spheres so that the spheres of one planet would not transmit their motion to those of another planet farther in. (E.g., you need 3 counter-acting spheres between Jupiter & Saturn, so that Saturn's innermost sphere will not transmit its complex motion to Jupiter's outer-most sphere.)

Cosmological Developments

Heraclides proposes that the earth rotates once daily, which explains why all celestial objects appear to circle the earth once daily.

Aristarchus proposed a heliocentric model: the earth orbiting the sun. However, there was no good reason for accepting it at the time.

One problem with the heliocentric model: No stellar parallax is observable.

Others attempted to calculate cosmological constants, including: The earth-sun distance, the earth-moon distance, the ratio between the two, the size of the earth. Notable:

Aristarchus' method for calculating (earth/sun distance : earth/moon distance). See diagram in book. You can determine C/B by trigonometry (it is Cos ). Aristarchus measured = 87, leading to B/C = 19. Modern value: 89.85, leading to B/C = 390.

[Note: The concept of error analysis had not been developed. A's method was 'theoretically' ok, but highly sensitive to error, as the above figures show.]

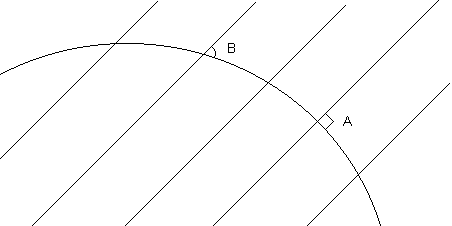
Eratosthenes estimates circumference of the earth: 252,000 stades (=28,600 mi.). [modern value: 25,000 mi.] [Method: Assumed sun rays are parallel, measured distance between 2 cities, and the angles a sun ray makes to the ground at each city at a fixed time. See picture below: Angle A is a right angle. The measure of angle B, and the ground distance between the vertices of A and B, can be used to determine the radius of the circle, according to the formula: r = 2d / ( - 2B). Amusing side note: The distance between A and B was measured by the time it took camels to travel the distance.]

Hellenistic Planetary Astronomy

Hipparchus: great Hellenistic astronomer. Most important contribution was introducing the idea of numerical precision -- i.e. quantitative, and not just qualitative predictions for an astronomical model.

Claudius Ptolemy (no relation to Alexander's general Ptolemy, who assumed control of Alexandria 500 years earlier): lived around 150 A.D. Inherited astronomical knowledge & methods from earlier astronomers, including Hipparchus. Aimed to account for apparent motions of planets using combinations of uniform circular motion. Aimed at quantitative predictions.

Ptolemaic model, dominant from 2^nd - 16^th century A.D.

1) The Eccentric Model: Planet moves uniformly in a circle with center C. Earth is located off-center (hence the term "eccentric" which in this context means 'off-center').

2) The Epicycle-on-Deferent Model (famous): Planet moves uniformly in a small circle, the 'epicycle.' In addition, superimposed on this motion, the center of the epicycle itself moves in a large circle around the Earth. This large circle is the "deferent."

Note: this explains retrograde motion.

3) The Equant Model: Planet moves in a circle. Earth is off-center. An equal distance from the center, but in the opposite direction, is the 'equant point'. The planet moves at varying speeds such that it sweeps out equal angles in equal times, as measured from the equant point. (So the angular velocity is uniform, relative to the equant point, but not relative to the center.)

These 3 models can be combined, particularly for Venus, Mars, Jupiter, and Saturn.

Why uniform circular motions?

The aim was to bring simplicity to the apparent chaos. Uniform circular motion is the simplest kind of motion [other than straight-line motion which won't work].

Aesthetic/religious reason: the perfection of the heavens demanded the most 'perfect' of motions.

Reliance on tradition & past authority.

Ancient mathematical methods could make predictions using circles, but they didn't know how to deal with other curves.

Ptolemy's system was the first system to offer accurate, quantitative predictions. Before the 16^th century, it was the only known theory to do so.

The Science of Optics

Optics: roughly, the study of how vision works.

Euclid: The eye sends forth some kind of rays; we see objects when the rays strike them.

Gave a geometrical treatment of optics, esp. laws of perspective. Ex.: Why farther away objects appear "higher" (think about drawing).

Ptolemy: Further developed Euclid's theory.

Unlike Euclid, Ptolemy was interested in the physical properties of the visual radiation.

More geometrical treatment of perspective.

Theory of reflection derived from Euclid: angle of incidence = angle of reflection.

Developed his own theories of refraction:

When light enters a denser medium, it is refracted away from the surface.

Ptolemy collected a lot of empirical data on refraction (using different media & different angles).

He tried to find a mathematical law relating angle of incidence & angle of refraction. He found some mathematical regularities, but did not discover the correct law. [Modern relation: Sine of the angle of incidence is proportional to the sine of the angle of refraction.]

The Science of Weights

Empirical law: weights on opposite sides of a balance beam balance when d₁w₁ = d₂w₂ (d₁ and d₂ being the distances of the weights from the fulcrum, w₁ and w₂ being their respective weights).

Problem: to explain this law.

The 'dynamic' solution:

Suppose weight A has weight of 10 and B has weight 20 and A is twice as far from the fulcrum as B.

Now, suppose they weren't in equilibrium, so one of them is moving up. Then A would move a distance of 2d in the time that B moved a distance of d (this is provable by purely geometric considerations). Vague idea: the greater velocity of A exactly compensates for the greater weight of B.

A rational reconstruction: On Aristotelian assumptions, the force required to move A at speed 2v would equal the force required to move B at v. That is why they are in balance. If the weight of A is changed (without changing anything else), it will put them out of balance, since then the weight required to move A up will be made either less or more than that required to move B up.

Archimedes proves the law geometrically, from two assumptions:

1) That equal weights at equal distances from the fulcrum are in equilibrium.

2) That if you have two equal weights anywhere on the beam, you can substitute a weight twice as heavy, located at their center of gravity (halfway between them).

Note: this is interesting because of the integration of mathematics & natural science.

Archimedes says that with a lever long enough, he could move the Earth.

Early Greek Medicine

Prior to about 400's B.C.:

Greek medical practice influenced by Egyptian & probably Mesopotamian practice.

Divine intervention is often supposed to cause disease.

The cult of Asclepius:

Asclepius: originally a (human) physician who probably lived around 1200 BC, later considered as the god of healing. [Note the difficulty of separating Greek myth from actual history. Asclepius probably existed, but not as a god of course.]

Temples to Asclepius offered healing, including both physical and 'spiritual' remedies.

Most famous was the healing dream, where you slept in the temple, and the god would either heal you in your sleep, or offer advice during your dream.

The symbol of Asclepius, a snake wrapped around a staff (the caduceus) remains as the symbol of the medical profession today.

Hippocratic Medicine

Hippocrates:

Lived around 400 B.C. Often called "the father of medicine."

His followers wrote over 60 medical books, the "Hippocratic writings."

Important contributions: The Hippocratic doctors represented 'learned medicine':

They opposed religious explanations of disease (i.e., divine intervention). Instead, they proposed natural causes for diseases & ailments.

They stressed observation, diagnosis, and prognosis. Thus,

They made detailed case studies.

On the basis of these, they could predict the course of a disease (prognosis).

Treatment:

Usually involved sensible things like good diet, exercise, sleep, bathing.

Occasional prescriptions for internal and external medicine.

The theory of the humors: This theory was held by many (not all) of the Hippocratic doctors.

There are four fluids (humors) in the body: Phlegm, blood, black bile, and yellow bile.

Disease is caused by an imbalance in the humors.

Humors are linked to the hot/cold and moist/dry dualities, leading to the conclusion that cold tends to cause certain diseases, etc. (For instance, a 'cold' is caused by coldness and wetness, which leads to too much phlegm in the body.)

There are 4 basic temperaments, arising from dominance of one of the 4 humors: phlegmatic (for phlegm), sanguine (blood), choleric (yellow bile), and melanholic (black bile). This is supposed to explain personality differences. The ideal personality has an even balance of humors.

The Hippocratic oath: According to tradition, Hippocrates established this oath to set a standard of ethical & professional conduct for physicians (though he probably didn't really write it). His followers all took the oath. Many physicians today still take modified versions of the Hippocratic Oath, which, in case you're curious, is as follows:

(Original version):

"I swear by Apollo Physician, by Aesculapius, by Health, by Heal-all, and by all the gods and goddesses, making them witnesses, that I will carry out, according to my ability and judgment, this oath and this indenture: To regard my teacher in this art as equal to my parents; to make him partner in my livelihood, and when he is in need of money to share mine with him; to consider his offspring equal to my brothers; to teach them this art, if they require to learn it, without fee or indenture; and to impart precept, oral instruction, and all the other learning, to my sons, to the sons of my teacher, and to pupils who have signed the indenture and sworn obedience to the physicians' Law, but to none other. I will use treatment to help the sick according to my ability and judgment, but I will never use it to injure or wrong them. I will not give poison to anyone though asked to do so, nor will I suggest such a plan. Similarly I will not give a pessary to a woman to cause abortion. But in purity and in holiness I will guard my life and my art. I will not use the knife on sufferers from stone, but I will give place to such as are craftsmen therein. Into whatsoever houses I enter, I will do so to help the sick, keeping myself free from all intentional wrongdoing and harm, especially from fornication with woman or man, bond or free. Whatsoever in the course of practice I see or hear (or even outside my practice in social intercourse) that ought never to be published abroad, I will not divulge, but consider such things to be holy secrets. Now if I keep this oath, and break it not, may I enjoy honor, in my life and art, among all men for all time; but if I transgress and forswear myself, may the opposite befall me."

(One contemporary version, approved by the AMA)

"You do solemnly swear, each by whatever he or she holds most sacred: That you will be loyal to the Profession of Medicine and just and generous to its members, That you will lead your lives and practice your art in uprightness and honor, That into whatsoever house you shall enter, it shall be for the good of the sick to the utmost of your power, your holding yourselves far aloof from wrong, from corruption, from the tempting of others to vice, That you will exercise your art solely for the cure of your patients, and will give no drug, perform no operation, for a criminal purpose, even if solicited, far less suggest it, That whatsoever you shall see or hear of the lives of men or women which is not fitting to be spoken, you will keep inviolably secret, These things do you swear. Let each bow the head in sign of acquiescence. And now, if you will be true to this, your oath, may prosperity and good repute be ever yours; the opposite, if you shall prove yourselves forsworn."

Hellenistic Anatomy and Physiology

3^rd century B.C.: Human dissection begins in Alexandria. This leads to advances in anatomy & physiology. They may also have used vivisection (dissection of live people).

Herophilus: Mainly interested in anatomy (study of the structure of the body & organs). He described the various internal organs. Interesting discoveries include:

Distinguished veins & arteries by the thickness of their walls. (This is fairly subtle.)

Studied the valves in the heart.

Erasistratus: Did more physiology (study of the functions of organs). Interesting contributions include:

Distinguished sensory & motor nerves.

Discovered that the pulse is a passive, mechanical response to the contractions of the heart.

His theory of digestion, respiration, & circulation:

Food is turned into blood in the stomach.

The veins carry this blood to all the parts of the body.

The arteries carry only 'pneuma', which we inhale through the lungs.

This pneuma is turned into a finer form of pneuma, 'psychic' pneuma, in the brain.

Psychic pneuma is carried to the rest of the body by the nerves. It causes sensation & movement.

Stuff moves through the body mechanically, according to the principle that nature abhors a vacuum.

Disease is caused by an excess of blood. Remedy: eat less. Alternately: Blood letting. [This last would seem to be a rather primitive theory, in comparison with his other achievements.]

Objection: how come blood comes out of arteries? When an artery is cut, the negative pressure causes channels between the veins & arteries to open, so that blood flows from veins into the arteries.

Hellenistic Medical Sects

After Erasistratus & Herophilus, numerous medical sects emerged with great debates among them:

'Rationalists': broad grouping of approaches to medicine, characterized by an inquiry into the hidden causes of disease. Some defended human dissection as a tool for discovering such hidden causes.

'Empiricists': Generally rejected human dissection & the search for hidden causes of disease. Instead, they thought one should just observe symptoms externally and prescribe treatments based on past experience.

'Methodists': Thought that disease was caused by tenseness or laxness of the body.

'Pneumatists': Built a medical philosophy based on Stoicism. [whatever that means.]

Galen and the Culmination of Hellenistic Medicine

Along with Hippocrates, one of the most famous physicians in history. Lived around 200 AD. Became the accepted authority on medical matters up to the Renaissance. Important contributions:

Produced a large number of books, summing up the state of medical knowledge at the time.

One of his innovations: To locate certain diseases in specific organs in the body.

Pursued his own anatomical & physiological investigations. His reliance on animals led to some mistakes. Famous mistake:

The rete mirabile: a mesh of blood vessels found in some ungulates (hoofed animals). He thought that it refined arterial blood to produce psychic pneuma. Actually, this structure does not exist in humans.

Correctly argued that the arteries carry blood.

His theories:

Accepted the theory of the 4 humors

Believed knowledge of anatomy & physiology was essential to medicine.

There are 3 basic physiological functions:

(i) A system for venous blood: Stomach & liver produce venous blood, which nourishes the bodily organs. Veins carry it to the rest of the body.

(ii) A system for arterial blood: Heart produces vital heat (which, of course, comes from 'fire'). The lungs help keep the right amount of heat in the heart (cooling it and providing 'air' to it). After the heart heats up the blood, the arteries carry it to the rest of the body, thus supplying life (vital heat) to them.

(iii) A system for psychic pneuma: This is produced by the rete mirabile. The nerves carry it to the rest of the body, endowing other parts of the body with the capacities for sensation and movement.

Galen's teleology:

He thought the human body, in all of its parts and aspects, was just perfectly designed for its functions. This showed the wisdom & goodness of the Demiurge (remember him from Plato's cosmology).

This made him popular during the very religious middle ages -- and not so popular in modern times.

[ Was this a reasonable idea on Galen's part, given what he was able to observe?]

VII. ROMAN & EARLY MEDIEVAL SCIENCE

Greeks and Romans

Rome takes over Greece sometime around 100 B.C.

Greek culture, however, takes over Rome. Learned Romans have to learn Greek philosophy and literature in order to be educated. (Ex.: all the Roman gods are just Greek gods renamed.)

Romans, however, knew only a popularized version of the Greek intellectual achievements, skipping the more technical aspects. Why? Compare the average American's understanding of modern science (and Greek science then was less practical than modern science).

Popularizers and Encyclopedists

3 important Roman scholars:

1) Varro: Wrote an encyclopedia, Nine Books of Disciplines. Describes the nine liberal arts: grammar, rhetoric, logic, arithmetic, geometry, astronomy, musical theory, medicine, architecture. [What, no metaphysics, no ethics?] Medieval schools adopted a shortened list (subtracting medicine & architecture) of the basic liberal arts. [This is a bit like our general education requirements, only more precise & detailed.]

2) Cicero: Famous Roman orator & writer. Tried to discover the truth by collecting and sifting through past expert opinion. [Contrast w/ scientific method.] [Famous saying of Cicero's: "There is no opinion so absurd that some philosopher has not held it."]

3) Pliny the Elder: Wrote dozens of books about scientific subjects, including about 50 volumes of history. Most important, & only surviving work: the Natural History.

It is a 37-volume encyclopedia of a variety of disciplines of natural science.

Pliny says it contains 20,000 facts, which he got from 2000 books, by 100 authors.

Contains some fantastic stories. See the picture of monstrous races on p. 141, for example.

Also contains useful records of the astronomical knowledge of the time.

Among other things, numerous species of plants and animals are described.

Pliny becomes the foremost scientific authority of antiquity, and his Natural History is preserved throughout the middle ages. He died during the eruption of Vesuvius (79 AD), when he decided to take a closer look and perhaps help the survivors (died from the fumes).

The "commentary tradition": a late ancient - medieval tradition in which education focuses on understanding certain specific, authoritative texts. Scholarship is commentary on these texts. [This happened especially with Aristotle & St. Thomas as authorities in the middle ages, after Aquinas.]

Notice how this goes against the ideal of science (in your physics class, you don't have to comment on Newton's Principia). But notice also that there are some areas where today we have a similar tradition (e.g. English & sometimes philosophy).

Martianus Capella: Roman compiler, after 400 AD. Became one of the principal authorities in medieval schools for the teaching of the 7 liberal arts.

[Liberal arts are those subjects fit for the general excellence of the intellect & soul; distinguished from practical arts. In medieval schools, the 'trivium' -- grammar, logic, rhetoric -- were taught first, leading to a B.A. You could then go on to learn the 'quadrivium' -- arithmetic, geometry (includes geography), astronomy, and music -- leading to an M.A.]

Martianus places Mercury & Venus on orbits around the sun (but not the other planets). [Why? Probably because of the way that Mercury & Venus are observed never to stray far from the sun, as the other planets do.]

Translations

After the death of Marcus Aurelius in 180, the Roman Empire is increasingly subject to civil unrest & economic decline.

[The cause of this "decline & fall of the Roman Empire" is a topic for debate among historians. It is often attributed to the increasingly unwieldy bureaucracy, as the Roman government tried to control more and more aspects of life in a too-large empire. The last Roman emperor is deposed by the Goths in the late 5^th century.]

Learning declines, partly due to a split between the (Roman) Western and (Greek) Eastern halves of the empire. Some scholars attempted to counter-act this, translating important Greek works into Latin for a more popular audience: including Boethius, an important translator (died in 524).

The Role of Christianity

Christianity started, of course, after Christ was born, in 4 BC., and spread gradually throughout Europe. Important events/people:

Tertullian (ca. 200): Famous fideist & influential on the early church. Believed faith was superior to reason. Famous saying: "I believe it because it is absurd" (Credo quia absurdum est). Thought that a Christian does not need to learn about classical philosophy, and that arguing with heretics or infidels was wrong. Just believe.

St. Augustine (ca. 400): Most influential of the church fathers. Viewed philosophy -- including natural philosophy of course -- as the handmaiden of religion.

[ Emperor Constantine (after 300) converts to Christianity, becomes emperor, institutes toleration of Christians & state support for the church. This is a major step in establishing its future control of Europe.]

[ Pace Lindberg, the Church has been a serious obstacle to scientific progress. Lindberg says it preserved some of classical knowledge -- because they thought it could be turned to Christian use. But they also stifled anything that they didn't think could be put to use supporting Christianity. Lindberg says science has often served as handmaiden to some ideology or practical end. But this is not true of, say Plato and Aristotle. Moreover, there's a big difference when you have an institution with coercive power, enforcing this relationship. Consider the famous example of Galileo.]

Roman and Early Medieval Education

Roman education, in the late Roman empire:

First stage: usually home schooling (by parent or tutor). Reading, writing, and basic math.

Second stage: (only for some boys) schooling in Latin grammar & literature, followed by rhetoric. Note that the reading of literature teaches Roman/Greek (pagan) culture.

Third stage: (for people with money & ambition) Study with a philosopher. But natural philosophy still receives but little attention.

During the decline of the empire, education also declines.

Christian attitudes:

Some Christians consider pagan culture a threat to Christianity (as offering an alternative worldview).

Others, however, value their own classical education, but try to turn it to Christian purposes.

Ca. 4^th century AD, monasteries start to replace Roman schools.

Monasteries are for the education of future monks (not ordinary people)

Reading & writing is necessary, for monks must study the Bible & commentaries on it.

Hence, monasteries preserve some literacy (among the monks), and some important books, including some classical works (but only ones the church finds useful for Christianity).

Keep in mind that the ruling function is the worship of God -- learning is encouraged exactly to the extent that it serves this function.

During the following several hundred years, natural philosophy stagnates -- almost nothing new happens.

[Lindberg makes apologies for Christianity, saying the monasteries preserved and transmitted classical learning. But the takeover of Western culture by Christianity was what made such 'preservation' necessary and made people uninterested in progress.]

Two Early Medieval Natural Philosophers

Saint Isidore of Seville: (about 600)

Wrote the Eymologies, an encyclopedia, based on pagan and Christian sources. One of the standard texts of the middle ages.

Preserves ancient view of cosmology: Isidore takes a geocentric view of the cosmos. The earth is spherical. Matter is composed of the 4 elements.

Helped convert the Visigoths to Christianity.

Saint Bede the Venerable: (about 700)

Wrote a series of textbooks for monks.

Best known for his history of England.

Why are these figures important?

Not because they discovered any important new ideas. Rather, they preserved learning during the Middle Ages, and they influenced how future Europeans would think about nature.

Learning and Science in Byzantium

Byzantium: What became of the Eastern half of the Roman Empire.

Capitol: Constantinople. Formerly 'Byzantium'; renamed after Constantine the Great made it the new capitol of the Roman Empire in 330. Became the largest & richest city in Christendom during the middle ages. (Now Istanbul, Turkey.)

Byzantium was much more stable than the western part of the Roman Empire. Classical knowledge declined less rapidly here, although there was little innovation.

There are a few examples of intelligent commentaries on Aristotle & Plato.

Plato is much more widely followed than Aristotle in the early middle ages. [Probably because Plato's philosophy is closer to Christianity.]

The Eastward Diffusion of Greek Science

Greek culture spread eastward (into Middle East & Asia):

First, with Alexander's conquests in the 300's b.c.

Alexander founded a number of cities during his military campaigns, most of them named "Alexandria" after himself. Of particular importance was the Alexandria in Egypt, home of the famous library.

Contribution of religion: Three competing religions:

Zoroastrianism : [An ancient Persian & Indian religion, based on the teachings of Zoroaster (a.k.a. Zarathustra). Good god: Ahura Mazda, associated with 'Truth'. Evil god: Angra Mainyu, who is evil by choice, having allied himself with 'Lie'. Human beings also must choose between good & evil. After death, good people will go to heaven, and bad people to hell. Hell is only temporary, though, until the final battle when evil will be defeated, and the evil souls purified. Fire is sacred in this religion. Most important virtue: truthfulness. Some Zoroastrians remain in Iran and India today (also called "Parsis").]

Christianity : [You all know about that.]

Manicheism : [Ancient religion based on the teachings of Mani, who thought he was the last in a series of prophets that included Zoroaster, the Buddha, and Jesus. Good & evil used to exist in separate realms. Human beings are the result of an invasion of the good realm by evil and a subsequent struggle between the two. The body is the evil part of humans and the soul the good part. The ultimate aim for people, in this religion, is to free the soul from the body, which will result from a knowledge of the realm of good (imparted by the divine prophets), and a renunciation of carnal (body-associated) desires. The people of highest spiritual attainment (the elect) can expect to ascend to the realm of Light and rejoin God after death. Others will be reborn. Eventually, everyone will be redeemed, the Earth will be destroyed, and good & evil will again be separate.]

These 3 religions all relied on sacred texts. For that reason, they had to cultivate at least some measure of learning.

Conflict in Christianity:

Nestorians: emphasized Christ's humanity. Nestorians helped spread Greek learning, translating some Greek texts into Syriac (an ancient Semitic language). [Held that Christ was one person with two natures. Said that Mary should not be called the "mother of God" (theotokos), but only the mother of Christ (christotokos). The church interpreted Nestorius as saying that there were two persons, Christ the man and the divine Christ.]

Monophysites: Held that Christ was God, not a man.

Both of these were condemned by the Church. [Current official doctrine: Jesus is a single being, who was simultaneously entirely human and entirely divine.]

The Birth, Expansion, and Hellenization of Islam

Islam founded by Muhammad in the 600's in Mecca. Muhammad claims to be a prophet, whose revelations are set down in the Koran.

[ Muslim doctrines:

Allah is omniscient, omnipotent, creator of the world. The Koran is the word of God & infallible. Mohammed is the last and greatest prophet in a series including Adam, Abraham, Moses, Jesus, and others. (Jesus was a prophet, not god.) The ultimate purpose of humanity is to worship God & create a social order free from 'corruptions.' The prophets are sent to guide humanity in the correct moral behavior. On the Day of Judgement, everyone will be judged according to their deeds, and rewarded with heaven or punished with hell. 5 central duties (the 5 pillars of Islam):

1. Profession of faith

2. They have to say 5 daily prayers.

3. Almsgiving (zakat) -- Muslims contribute some of their money for charitable purposes, including helping the poor, helping to spread Islam, and supporting jihad (holy wars). Originally collected as a tax by Muslim states.

4. They must fast during daytime throughout the month of Ramadan.

5. Every Muslim must make a pilgrimage to Mecca at least once in his lifetime.

The goal of Muslims is "God's rule on Earth." Muhammad believed in the necessity of holy war and compulsory conversion to achieve this.]

Muhammad takes over Arabia. After his death, Muslim forces take over most of the Middle East, including Persia & Egypt, later taking over North Africa and Spain.

They use educated Persians to staff their bureaucracy. This is one way Hellenistic culture got a chance to influence Islamic culture.

Translation of Greek Science into Arabic

2 languages widely used in the middle east:

Syriac (ancient Semitic language, closely related to Hebrew). The major language in use in the Middle east up to the 7^th century.

Arabic: comes into use increasingly after the Arab conquests of the 7^th century.

Important translator: Hunayn ibn Ishaq: a Christian Arab. Together with his son & nephew, Hunayn translated a large number of Greek works into Arabic & Syriac, including works of:

Galen, Hippocrates, Plato, Aristotle. Hunayn's son translated Euclid's Elements & Ptolemy's Almagest.

By 1000 A.D. most of the Greek works existed in Arabic versions.

The Islamic Response to Greek Science

In Islamic culture, knowledge is not valued for its own sake, but for the sake of some other end -- e.g., if it can promote religious purposes, help run the state, or achieve other practical ends.

Ex.: Medicine is practically useful. The first Greek texts translated were medical texts.

However, Greek thought is integrated: in order to understand Greek medical theories, one has to understand something of Greek metaphysics/physics (e.g., the 4 elements). This may explain why so many Greek texts were translated.

Historians are divided over how well Islamic culture received Greek science. However, we can say at least this much: the reception was neither overwhelmingly positive, nor a complete rejection. It is also clear that at most, Greek science was seen as a useful handmaiden to other pursuits.

The Islamic Scientific Achievement

[ Duhem vs. Lindberg: Duhem says that there is no Islamic science; Lindberg says that the Muslims made many contributions "of the utmost importance and originality," but does not list them.

What seems fair to say is that Islamic science was founded on Greek science, and that the Islamic contribution consisted in extensions of and efforts to perfect the theories of the Greeks, rather than entirely new ideas. This assessment is borne out even by the examples Lindberg cites of their allegedly important contributions.]

The Decline of Islamic Science

Islamic science declines after the 13^th century. Why? 2 speculations:

Increasing opposition from traditional elements in Islam, who saw Greek-inspired science as a threat to religion, or merely as useless.

War with Christians in Europe (esp. Spain) & Mongols to the east. Science generally flourishes only in times of peace & prosperity.

The Middle Ages

The middle ages divide into 3 parts:

Early : ~500-1000 a.d.

Transition period ('middle middle ages'?) : ~1000-1200.

Late or 'high' middle ages : ~1200-1450. 1450 is about the beginning of the renaissance.

Carolingian Reforms

In general, medieval times see very little science --

Learning happens mainly in the monasteries

The focus is mainly on theology. Greek logic & metaphysics make an appearance due to their relevance to theological problems. 2 examples of medieval problems:

The nature of the trinity.

Problem of divine foreknowledge. [God's omniscience seems to be incompatible with the existence of free will.]

The Carolingian Empire:

Charles the Great (a.k.a. Charlemagne, from Latin "Carolus Magnus") rules it, ca. 800.

The Empire includes most of France, and parts of central Europe, including Rome by the time of Charles' death (he expanded the empire).

More about Charlemagne:

[ Son of the amusingly named 'Pepin the Short'.]

Proclaimed 'emperor of the Romans' by the Pope in 800 -- in an attempt to recall the past glory of the Roman Empire. (This inaugurated the practice of the church proclaiming 'Roman emperors', which later led to the 'Holy Roman Empire' which endured for almost 1000 years.)

Charlemagne's educational reforms:

Builds a palace & establishes a palace school

Brought Alcuin from York to be head of the palace school.

This results in an increase in education among the clergy. Alcuin's school focuses on the 'trivium' and 'quadrivium.' (See notes on ch. VII, p. 24, above.)

Orders monastery & cathedral school established throughout the realm.

Important scholar later on (~1000): Gerbert:

Eventually became Pope Sylvester II.

Studied mathematics extensively and taught it to others. (He had teaching posts for a while.) He probably used his power in the church to advance the cause of mathematical education as well.

The Schools of the Eleventh and Twelfth Centuries

After 1000, a revival of learning begins.

Causes: Several factors may have had something to do with it, including increased political stability, increased prosperity, greater population, and especially, urbanization.

Note that schools generally appear in large cities. (Except for monastic schools.)

Hence, more non-monastic schools appeared in the mid-middle ages.

This meant a broader focus, as compared with the monastic schools which were almost entirely focused on theology.

Classical learning undergoes a revival. Medievals appreciate the likes of Virgil, Cicero, Plato, Aristotle. Aristotle is studied for his logic. Plato's cosmology is studied.

Classical learning is a supplement to (rather than replacing) Christian learning centered on the Bible.

Theology becomes more rationalistic. Case in point: Saint Anselm. Existence of God can be demonstrated through reason.

[ Anselm's proof of the existence of God: The Ontological Argument.

1. God = A being than which none greater can be conceived. (Definition of 'God')

2. God can be conceived to exist. (Premise)

3. An existing god would be greater than a non-existent god. (Premise)

4. Assume God does not exist.

5. A god that existed would be greater than God. (From 3, 4)

6. Therefore, something greater than God can be conceived. (From 2, 5)

7. That is: a being than which none greater can be conceived, is a being than which a greater can be conceived. (From 1, 6) Which is absurd.

8. Therefore, God exists. (From 4-7, by reductio ad absurdum.)]

Slightly later thinker: Peter Abelard. Collects a set of conflicting opinions of church fathers on theological topics. Uses them to stimulate philosophical reasoning about theology. Note that Abelard's use of reason, like Anselm's, is purely in support of Christianity. Nevertheless, some saw it as a danger, because reason may not always turn out to be congenial to the faith.

This raises the question of the relation between natural knowledge (through reason) and revelation. Can the revealed truths of the Bible also be known through reason?

Natural Philosophy in the Twelfth-Century Schools

Plato especially popular in 12^th century, esp.: The Timaeus, Plato's work on cosmology.

Thinkers such as Thierry of Chartres attempt to reconcile Plato's account of cosmology w/ the Biblical account in Genesis, esp.: P's account of the creation of the cosmos (his 'cosmogony').

The 12^th century sees a movement towards naturalism: i.e. attempts to explain things by natural causes, rather than divine intervention.

This is not a rejection of the existence of miracles -- just a doctrine that miracles should only be used to explain things when all natural explanations fail.

Some view this as a theological danger. Once this principle is accepted, you might find yourself denying miracles altogether.

William of Conches, one of the naturalists, argues: God would, and did, create a perfect & orderly nature -- he contrived to bring about the ends that he wished, for the most part, through the operation of nature. This illustrates, rather than detracting from, his great wisdom & power.

God is the creator of nature & natural laws themselves. Hence, natural explanations actually are explanations by reference to God (just a particular way God did things).

[ Note the remark (p. 201) that "all things that are in the world were made by God, except evil." This alludes to the famous problem of evil in theology.]

This naturalism was accompanied by increased interest in 'natural man.' Includes greater confidence in the power of reason. [After all, God gave us reason to understand the world, didn't he?]

Astrology also on the rise. Note that astrology was conceived as another case of the operation of natural causes.

The Translation Movement

A number of Greek works are translated (into Latin) in the 12^th century.

In Spain, recently recaptured from the Muslims by the Christians, works are translated from Arabic, including the likes of Ptolemy's Almagest, & Euclid's Elements. [So they were translated from Greek to Arabic by the Arabs, then from Arabic to Latin.]

In Italy, translations from Greek into Latin are done.

Works are selected for their utility. So astronomy & medicine are first. But mathematics is needed to understand astronomy, and Greek medicine rests on Greek physics & metaphysics.

The Rise of Universities

Some cities become known as centers for learning, esp. Paris, Bologna, & Oxford. Teachers & students gather there.

Teachers start to form guilds or unions (Latin: "universitas"). These are the first 'universities'. Note that the university was initially just a union of teachers -- not a set of buildings or land.

Universities in Oxford, Bologna, Paris established circa 1200.

Universities gained influence with government & church, to get their protection & privileges.

Gradually, they evolve more formal structure -- e.g., definite curriculums & degrees.

Subjects in the university:

Liberal arts : This gets you the B.A. or M.A. The trivium & quadrivium remain but with less importance. Required philosophy learning: a) Moral philosophy, b) Natural philosophy, c) Metaphysics.

Graduate schools in specific subjects: Medicine, Law, Theology.

At the end of the 12^th century, Aristotle starts to be taught in the universities. In the 13^th century, he fairly takes them over.

Teaching is from central (mainly Greek) texts.

Unlike the ancient Greek schools, the medieval universities teach pretty much the same subjects, from the same texts. This standardization of learning resembles modern universities.

Medieval teachers have considerable freedom of thought, according to Lindberg. Any doctrine can and will be subjected to minute logical examination. [Of course, this is within the universally accepted framework of Christianity -- you wouldn't be free to proclaim atheism!]

X. THE RECOVERY & ASSIMILATION OF GREEK & ISLAMIC SCIENCE

The New Learning

The educational revival after 1000 a.d. started with a revival of classical (Greek & Roman) knowledge.

This revival grew stronger in the 12 & 13^th centuries.

The 'new' ideas posed challenges for how to integrate them into existing theological beliefs -- particularly the more philosophical works.

Aristotle in the University Curriculum

Aristotle's influence in the schools grows after 1200, partly through the commentaries of the Muslim philosopher Avicenna.

Problem in Paris: church finds some of Aristotle's work dangerous (there are accusations of pantheism). Pope Gregory appoints a commission to purge the objectionable parts. But the commission doesn't seem to have done it.

The influence of the ban wears off in a few decades, and in 1255, Aristotle becomes a mandatory part of the curriculum in Paris. Aristotle is taking over.

Points of Conflict (between Aristotle & Christianity)

Aristotle says the universe is eternal (in the past direction).

Contradicts Christian doctrine of creation.

Aristotle has objects acting according to fixed natures. Aristotle has a 'Prime Mover' (a being that moves other things but is not itself moved; the ultimate cause of all motion); however, the Prime Mover is unchanging and its effects are regular & predictable. Prime Mover is also impersonal; doesn't care about human affairs.

Contradicts concept of miracles.

May contradict concept of a personal God who loves & helps individual humans.

Aristotle has some astrological beliefs (the stars influence human affairs)

May conflict with doctrine of free will.

Aristotle's 'soul' is simply the form of the body.

Contradicts immortality of the soul.

Averroes developed a concept of an immortal soul; however, it was a sort of collective soul (there is one shared by all humans).

Again, contradicts Christian notion of personal immorality (you will survive as an individual, into the afterlife).

These conflicts seem to reflect a more fundamental one: The rationalistic and naturalistic tendencies of Aristotle, as contrasted with the church.

Some theologians worry that Aristotle is supplanting Christianity.

Resolution: Science as Handmaiden

Aristotle's influence proved irresistible, basically because he was such a great philosopher. His writings provided a comprehensive understanding of the natural world, and reality in general. (He wrote about physics, metaphysics, ethics, biology, perception, logic, aesthetics, & cosmology.)

Grosseteste: commented on Aristotle & tried to combine Aristotelian doctrines with neoplatonism.

Roger Bacon: Tried to convince the church that Aristotle was useful for theology. Theology is the queen of the sciences.

St. Bonaventure: basically agrees w/ Bacon, but is more cautious.

Thinks Aristotle is just wrong on the points of conflict listed above, because Aristotle didn't have the benefit of divine illumination.

Held that God was active in every case of cause & effect in the natural world. (The cause produces the effect only because God wills it.)

[ Side note: 2 mendicant orders at this time: Franciscans (founded by St. Francis) & Dominicans (founded by St. Dominic). Took vows of poverty. Bonaventure became head of the Franciscans. Albert & Aquinas were Dominicans.]

Albert the Great (St. Albertus Magnus, patron saint of natural scientists), 1200's: taught in Cologne & Paris.

Composed a comprehensive interpretation of the Aristotelian corpus. Basically accepted Aristotle, but corrected Aristotle periodically on the basis of his own observations. Wrote over 8000 pages on Aristotle.

Rejected the eternity of the universe as philosophically absurd.

Rejected doctrine of soul as form of the body.

Took a quasi-naturalistic approach: although God ultimately causes everything, God normally works through natural mechanisms, and we should try to understand these.

Did not think that philosophy and theology could conflict, if carried out properly.

Thomas Aquinas (St. Thomas): Student of Albertus Magnus. Called a 'dumb ox' by fellow students.

Natural reason & revelation are both legitimate means of knowledge, and they do not conflict. Both are given by God.

Philosophy can assist theology by (a) proving some basic propositions of the faith, (b) answering objections to the faith.

Famous book: Summa Theologica. Comprehensive theological treatise, defending Christian doctrine against various objections. [Takes the form of a question, followed by arguments against the Christian doctrine, followed by quotations from some authority (usually the Bible), followed by arguments defending the theological item in question, followed by answers to the objections.]

Synthesized Aristotle w/ Christianity. Philosophy of "Thomism" later became the official philosophy of the Catholic church.

[ Aquinas claimed 5 proofs for the existence of God. They were based on (a) motion, (b) efficient causes, (c) necessity & contingency, (d) gradations of goodness, (e) teleology in nature.]

Radical Aristotelianism and the Condemnations of 1270 and 1277

A few radical philosophers depart from Thomas & Albert, notably Siger:

Maintains that philosophy can come into conflict w/ theology. Argues that reason leads to the doctrine of the eternity of the world.

Professes to side with faith in such conflicts, but he may have been lying to placate the church.

In 1270, the bishop of Paris issues condemnations of 13 propositions allegedly taught by Siger.

In 1277, he issues a longer list, including 219 propositions, the teaching of which is grounds for excommunication. They include:

Eternity of the world

Monopsychism

Denial of personal immortality

Denial of free will

Various propositions about things God couldn't do, such as creating multiple universes, moving the celestial sphere, or making an accident w/o a subject. (B/c Aristotle showed these things to be impossible.)

The significance of this: a reactionary, anti-Aristotelian move.

The Relations of Philosophy and Theology after 1277

No one aimed to completely remove Aristotle, but only to discipline Aristotelian philosophy.

Aristotle's influence continued to grow, and Thomas was made a saint in 1323.

More about divine omnipotence. Historians have disputed whether the effect of this doctrine was

a) To impede natural science, because the universe need not be governed by predictable laws, since God could do anything he likes. Or

b) To promote natural science, because in order to find out which world God actually did create, one would have to do empirical observation.

Neither of these seems quite right.

1. Web page of William Lane Craig, contemporary defender of the Cosmological Argument:

http://www.leaderu.com/truth/3truth11.html

2. Bertrand Russell's famous essay, "Why I Am Not a Christian":

http://www.geocities.com/Athens/Delphi/2795/whynot.htm

1. Could God make a stone so heavy he couldn't lift it?

2. How can God be 'all-powerful', since he is incapable of being corrupted, or doing evil? (Anselm discusses this question.)

3. Conflict between divine omniscience & human free will. If God knows what you are going to do before you do it, are you still free not to do it?

4. The problem of evil: a) If God is omniscient, then he is aware of evil; b) if he is all-powerful, he is able to remove it; c) if he is all-good, then he is willing to remove it. But if God is aware of evil, and both willing and able to remove it, then how does evil exist?

The Structure of the Cosmos

Early medievals accepted Platonic cosmology (based on Plato's Timaeus).

Later, Aristotelian cosmology supplanted Plato's, in the areas where they differed. Ex.:

Plato had all the physical world composed of the same kind of stuff (the 4 elements).

Aristotle had the celestial (superlunar) realm composed of a different sort of stuff, 'ether' (a.k.a. 'quintessence').

Aristotle's system of planetary spheres.

More elements of medieval cosmology:

The cosmos is a large but finite sphere

Earth is at the center

The cosmos was created (not eternal).

The Heavens

What is outside the celestial sphere?

According to Aristotle, (a) there is no void space, but (b) the cosmos is a finite sphere. It follows that (c) space is a finite sphere.

Medievals rejected this for two sorts of reason:

a) A religious reason: In the condemnation of 1277, it was said that God could move the cosmos. It seems to follow that there is a space to move it into, and further, that a void space could exist, since a void would be left behind by the cosmos' motion.

b) Anyway, what would happen if you got to the edge of space and then you stuck your hand out?

Where is the celestial sphere?

According to Aristotle, location is a relationship of a thing to its container. As a result, the celestial sphere has no location (nor does the universe as a whole).

Many medievals found this unbelievable. One solution is to redefine location as a relation to the thing contained, rather than the container.

Problem: the Bible makes a distinction between the heavens and the firmament, but this doesn't fit w/ Aristotelian cosmology. [Gen. 1:1: "In the beginning God created the heavens and the earth." Genesis 1:6-7: "And God said, 'Let there be an expanse between the waters to separate water from water.' So God made the expanse and separated the water under the expanse from the water above it."]

Some postulated additional spheres, above the planetary spheres (but before the fixed stars), including a sphere of water, but possibly not the same kind of 'water' we have on earth.

Nature of the spheres:

Early thinkers thought of them as composed of fire.

Later, under the influence of Aristotle, people thought of them as 'aether'.

They fit together perfectly (remember: no void space) and rotate without friction between them.

Unmoved movers:

Acc. to Aristotle, there was an 'Unmoved Mover' for each of the planetary spheres. (Remember that all motion requires a cause.)

The 'Prime Mover', the unmoved mover for the celestial sphere, was identified with God by the medievals.

Q: What about the other unmoved movers? Some identified them with angels. Others denied the need for such additional unmoved movers.

What about Ptolemaic epicycles?

Some medievals made the spheres thick enough to contain the planets on their epicycles. (Derived from the Muslim astronomer Alhazen's suggestion.)

This, given how the spheres are tightly packed, enabled calculations as to the diameter of the heavens.

Result: The celestial sphere is 73 million miles in radius. This figure survived until Copernicus' revision in the 16^th c.

The Terrestrial Region

A form of geographical knowledge: the 'periplus':

A list of major landmarks encountered as one travels along a coastline. Pliny & St. Isidore provided them for the European & African coastlines.

Division of the earth into climes:

Frigid zones (arctic & antarctic)

Temperate zones, northern & southern.

Europeans & all known peoples live in the northern temperate zone.

The existence of people in the southern temperate zone, called 'antipodeans', was disputed (considered heresy by the church).

Torrid zone (around the equator. Uninhabitable due to heat.)

Medieval maps: Initially, they did not use the concept of scale, nor of representing actual distances on the earth by distances (in the same ratios) on the paper.

Ex.: The T-O maps. (See p. 255 in the book). They are schematic. (In modern terms, we might say they only represent topology.)

Later development: Portolan charts. More like modern maps (more 'realistic').

Used for navigation at sea.

The lines show compass directions from one point to another. Useful in conjunction with a compass, which was invented around the 12^th century.

Does the earth rotate?

Rotation of the earth would produce the same astronomical observations. Important point: astronomers only observe relative motions.

Advantage of rotating earth: greater simplicity

Arguments against a rotating earth:

1. An arrow shot upward falls to the ground at the same spot. (Buridan's argument)

Oresme responds. Uses the example of a person inside a (perfectly smoothly) moving ship, who is unaware of the motion. (Compare to Galileo's argument.)

[2. If the earth were rotating, the centrifugal force would throw everything off the equator. (Ptolemy's argument)]

The Greek & Islamic Background to Western Astronomy

Differences between astronomy & cosmology:

Astronomy more mathematical. Derived from Ptolemy's Almagest.

Cosmology was more focused on physical considerations. Derived from other texts, such as Aristotle & the Bible.

Astronomical instruments:

Large quadrants (13^th c.)

Sextant (18^th c.)

Astrolabe. (From 100 b.c. Modified by Muslims to be used for astronomical calculations -- modified form included a simple map of the heavens & moving parts to simulate movement of heavenly bodies. (as in picture on p. 265 in the book)

Muslim astronomers criticize Ptolemy's astronomy, as lacking a physical basis.

Averroes wants to return to Aristotelian spheres.

Alhazen tries to reconcile Aristotelian spheres w/ Ptolemaic epicycles.

Astronomy in the West

In the early middle ages, there was little astronomical knowledge.

The Christians gained astronomical knowledge through contact w/ the Muslims in Spain, incl.:

the astrolabe, making quantitative astronomy possible

translations of ancient astronomical works, esp. Ptolemy, leading to the teaching of Ptolemaic astronomy in the schools.

Astronomical knowledge grows increasingly sophisticated after this (though confined to a relatively few practitioners).

Astrology

Astrology = the study of the effects of the heavens on the things on earth.

Observational evidence for the influence of the heavens on the earth:

Heavenly bodies are the source of light & heat

The seasons are connected w/ the sun's motion around the ecliptic.

The tides are connected w/ the moon's orbit.

The pole of the celestial sphere exercises magnetic attraction (compass needle points towards it).

Religious support:

The heavens have long been associated w/ divinity, and divinity has been thought to influence human affairs, going back to ancient times.

There was also a widespread belief that celestial events were 'omens' of terrestrial events, going back to ancient Mesopotamia. This eventually developed into the idea that the celestial configuration at the time of your birth indicated the future course of your life.

The Greeks also thought the heavens affected the earth.

Plato: the Demiurge delegated to the planetary deities the task of creating parts of the sublunar realm.

Aristotle: the Unmoved Movers were also the source of terrestrial motion.

Stoics: thought of the whole universe as an organic whole.

People (from ancient through medieval times) saw these sort of influences as of a piece with the influences the heavens allegedly exert on the weather, and on individual people.

Objections to astrology:

Augustine worried that astrological beliefs threatened the doctrine of free will.

Celestial influence on the body was ok, as long as one preserves freedom of the will.

This attitude was followed by medieval thinkers. The general view was that astronomical events did have an influence on human affairs in a general way, but that they did not determine an individual's decisions.

[ Philosophical reflection: This is another chapter in the perennial determinism / free will controversy. Free will has been threatened by (a) the Fates (in Greek mythology), (b) God's omniscience, (c) astrology, and today (d) modern biology, psychology, and/or physics. Are the modern fears of determinism better-founded than those earlier ones?]

XII. THE PHYSICS OF THE SUBLUNAR REGION

Note that medieval 'physics' was not necessarily addressed to the same questions and purposes as modern 'physics.'

[ Compare Thomas Kuhn's concept of 'paradigms' and 'paradigm shifts.' Kuhn says that different paradigms are 'incommensurable.']

Matter, Form, and Substance

Material objects as matter + form. 2 aspects to form:

'substantial form' (essential properties)

'accidental form' (accidental properties)

Primary matter: matter, apart from its form. Matter without properties. (This cannot actually exist.)

Corporeal form: invented by later commentators. Gives matter its 3-dimensionality. [This is essential to its being a body.]

Elemental form: 4 elemental forms distinguish the 4 elements from each other. Each elemental form is associated with a combination of the basic qualities (hot vs. cold, and wet vs. dry). E.g., when matter has the hot & dry elemental form, you get the element 'fire'.

Elements can be transmuted, if the matter loses one form and gains another.

Actual matter must have at least elemental form. It can, in addition, get other forms imposed on it, as when a bunch of matter gets formed into a statue. [Note that there are different levels of composition here: the statue composed of marble, which is composed of the 4 elements, which are composed of primary matter. At each level, you have a form imposed on the stuff of the lower level, in order to get it to the higher level.]

Combination and Mixture

Elements get combined into "mixta" (mixtures). Almost all the substances we encounter (wood, granite, etc.) are mixta.

Mixta are not simply one element next to another. Rather, the elements are completely mixed. The new substance has a new form, whose properties are determined by the properties of the component elements & their proportion.

Medievals had debates about the relationship between the elemental forms and the form of the mixtum--

Do the elemental forms still exist in the mixture? Perhaps only potentially? In a weakened form?

Doctrine of minima: The smallest parts of a mixtum that still have the properties of that mixture. Different from atomism:

atomists thought there was void space between atoms

the atoms could not in principle be divided.

all atoms were of the same stuff.

atoms lacked the properties of macroscopic materials.

None of these things is true of minima.

Alchemy

[ Alchemy first began in ancient Egypt. It became popular in the middle ages, as another thing the Europeans got from the Arabs.]

Metals are compounds of sulfur & mercury, formed under the influence of heat inside the earth.

You get more or less 'perfect' metals, depending on the purity of the sulfur & mercury, their proportions, and the degree of heat.

'Noble metals' : the more perfect (& valuable) metals, such as gold, silver, platinum. Less corruptible. Gold is the most perfect metal.

Less perfect metals like iron or copper are 'base' metals.

Main goal of alchemy: to transform base metals into gold.

Interesting substances:

The 'philosopher's stone' : a legendary substance so perfect that it could transform base metals into gold. Alchemists tried to figure out how to make one.

[ Aqua regia : a liquid that dissolves noble metals, particularly gold. (Roger Bacon thought gold dissolved in aqua regia was the elixir of life.) Actually a mixture of hydrochloric & nitric acid.]

Techniques used by alchemists:

Alchemists developed chemical processes:

Solution

Calcination (heating a substance, without melting, in order to drive off its volatile components)

Fusion (melting things; also, using heat to combining 2 substances into one, as in alloys)

Distillation

Putrefaction (decomposition caused by, in modern terms, enzymes & bacteria)

Fermentation (chemical changes caused by enzymes, esp. caused by bacteria, molds, and yeasts; produces alcohol, among other things)

Sublimation (converting a solid directly to a gas)

They produced apparatus for doing these things: furnaces, various kinds of flasks & other containers, and the alembic (apparatus for distilling).

This was the beginning of chemistry later on. However, it also developed into a kind of mystical, worldview (modern day 'alchemy' is a sort of new age phenomenon).

Change and Motion

There's lots of change in the Aristotelian world:

1) Generation & corruption (coming into & going out of existence)

2) Alteration (change of qualities)

3) Augmentation & diminution (change of size, or quantity)

4) Local motion (change of place)

Medievals had a whole different conceptual scheme from classical physics, which is complex and hard to get into. We'll just look at a few parts of it.

The Nature of Motion

First question to ask in any subject: what exists (relevant to that subject)? Then you can ask what properties they have, how they're related to each other, and so on.

In what way does motion exist? 2 views:

"flowing form" view: there's just the object and its successive places.

"flow of a form" view: there's also another thing called the 'motion' of the object.

William of Ockham: held the first view. One way to view this dispute:

"Every motion is produced by a mover.": for Ockham, this really means "Every thing that is moved, is moved by another thing." The substantive 'motion' is like a fictitious entity [sort of like 'the average man'].

[ Important : "Ockham's Razor": Principle enunciated by Ockham, "Entities must not be multiplied beyond necessity." Later became a central principle of scientific method, but with different sorts of applications.]

John Burridan supported the 2^nd view. Argument:

God could make the whole cosmos rotate. This would not be possible on the 'flowing form' view, because there is no succession of different places.

[ A more modern way of formulating the issue: Suppose an object existed for a single moment of time. Could it, at that moment, be in a state of motion (i.e., having an instantaneous velocity)? The modern physical view, where state of motion is defined in terms of a derivative, seems to be "no."]

The Mathematical Description of Motion

Ancients lacked a mathematical description of motion. They saw distance & time as measurable quantities, but not 'velocity'.

Dynamics (about causes of motion) vs. kinematics (just about the nature of motion).

The Merton group: group of scholars from Merton College, Oxford. (1300s)

Developed concepts of

velocity: uniform & non-uniform

acceleration

Discovered theorems about motion.

Foundation of mathematical concept of velocity:

Qualities have intensity. This is a concept of degree. For example, 'hotness': different degrees of temperature.

They also have extension or quantity. This depends on how widely distributed the quality is. Example: concept of the 'quantity of heat' in a body. (Note modern distinction between temperature & heat.)

The same is true of motion, because motion can be viewed as a kind of quality of a body.

'Intensity' of motion = velocity.

Nicole Oresme develops technique for graphing qualities:

A horizontal line represents the subject, with a vertical line representing intensity of the quality. Shape of the graph shows distribution of the quality through the subject.

Total quantity is the area of the graph.

Example: how to represent a heated rod.

Example: motion of a rotating rod.

Example: A body moving as a unit, but nonuniformly.

Subject line becomes time, rather than spatial extension.

Pictures on p. 299 show various kinds of motion. (Note: velocity is a scalar here, not a vector. They didn't have vectors.)

So, quantity of motion is the area of the graph: which is the distance traversed.

This is cool: Makes it possible to apply geometry to claims about motion. Samples:

The 'Merton Rule' or 'mean speed theorem'. If a body accelerates uniformly from v1 to v2, then it covers the same distance as a body travelling at (v1+v2)/2 over the same time. See picture on p. 300.

A second theorem: In a uniformly accelerated motion, the distance a body travels in the 2^nd half of its motion = 3 times the distance it travels in the first half.

This was done as pure mathematics.

Importance: establishes a conceptual framework & the idea of mathematical treatment of motion, which will be used by later thinkers such as Galileo & Newton.

The Dynamics of Local Motion

All motion requires a mover. 2 kinds of motion:

Natural (caused by nature of the body)

Forced (caused by external body)

Problem: In natural motion, the mover does not seem sufficiently distinct from the thing moved.

Problem: How to explain projectile motion. Why does an object keep moving when you throw it.

Aristotle: The object is pushed along by the medium.

Alternative: the thrower endows the object with an internal motive force, or "impetus".

This is distinct from the motion itself.

Impetus is 'corrupted' [or dissipated] by resistance.

This could explain motion of the heavens.

Measured by quantity of matter x velocity

The Quantification of Dynamics

Modern summary of Aristotle's view of falling bodies:

v F/R

Leads to the conclusion that a void is impossible.

Criticized by Philoponus, on empirical grounds. There is very little difference in velocity between heavy & light objects. He decided that, in a vacuum, a body would have a certain natural velocity, determined by weight. But in air, the resistance of the medium slows down heavier bodies more (?), leading to the observed results.

Thomas Bradwardine criticizes alternative accounts on mathematical grounds:

v F/R. Problem: predicts that if F=R, the body still moves.

v F - R. Problem: fails to predict that doubling F and R leaves the velocity unchanged.

Bradwardine's solution: To double the velocity, you have to 'double' the ratio F/R (but this really means squaring it, in modern terms).

[In modern terms: v log (F/R)]

The Science of Optics

Ancient optical theories were of 2 kinds:

Intromission theories: Something is taken into the eye, from the external object. This was held by people more interested in physical/physiological aspects of vision. (Aristotle)

Extramission theories: The eye emits something out towards the objects. Held by people interested in mathematical aspects. (Euclid, Ptolemy)

Alhazen: (Muslim scientist, ~1000 a.d.)

Attacked extramission theories. Arguments:

How could bright objects injure the eye?

Implausible that the eye could emit something filling up all the space up to the fixed stars.

Appropriated the visual cone, but used with an intromissive theory.

Used a concept of incoherent radiation for this purpose. (Radiation emanates from each point on the luminous body, in all directions.)

Each point of the eyeball receives rays from every point on the visible object. Why doesn't this lead to just a jumble in the eye? Answer: only the rays striking the eyeball perpendicularly are seen.

This influenced Western scholars after Alhazen's work was translated, around 1200.

Roger Bacon took on Alhazen's theory.

Attempted to reconcile intromission & extramission theories, by proposing that extramitted rays prepare the medium to receive the rays from the objects.

NOTES ON POST-MEDIEVAL SCIENCE

Some important scientists & discoveries:

I. Nicolaus Copernicus

Developed his heliocentric conception of the cosmos around 1510 but didn't publish it, probably for fear of criticism.

Wrote his famous defense of the heliocentric system, On the Revolutions of the Celestial Spheres in 1530, but it wasn't published until shortly before his death, in 1543.

Copernicus' system:

Earth rotates on its axis daily and orbits the sun yearly.

Kept the planetary spheres & the sphere of the fixed stars, but they are centered on the sun. The sphere of the fixed stars is stationary. The planets orbit the sun.

However, Copernicus' system was initially less accurate than the Ptolemaic system, and only slightly simpler.

The system was not accepted at first. There were only 10 Copernicans before 1600 (including Kepler & Galileo).

II. Tycho Brahe

Another astronomer, later in the 1500s.

The king of Denmark & Norway provided him funds to build an observatory, where he pursued his astronomical observations (until the next king took it away).

Brahe is known as a meticulous observer.

Discovered errors in the standard astronomical tables and corrected them.

Catalogued 700 stars. Made the most accurate measurements of stellar positions to date.

Proposed a compromise between Copernican & Ptolemaic astronomy: the planets orbit the sun, while the sun orbits the earth. The fixed stars also orbit the earth.

Provided data that enabled Kepler to formulate his laws.

III. Johannes Kepler

Kepler was Brahe's assistant at the end of Brahe's life (1600). Kepler lived into the early 1600s.

Accepted Copernican system. Initially he used circular orbits. Proposed that the sun emits a force that diminishes with distance and that pushes planets around in their orbits.

Later figured out that the orbits were elliptical.

Kepler's laws of planetary motion:

1. Planets move in elliptical orbits, with the sun at one focus.

2. A line drawn from the planet to the sun sweeps out equal areas in equal times.

3. R³/T² is a constant for all the planetary orbits, where R=the average distance from the sun and T=the orbital period.

Based on Brahe's data, Kepler found the Ptolemaic system to be in error, and his own system more accurate.

Heliocentric system was still not generally accepted when he died.

IV. Galileo Galilei

Lived into mid 1600s.

Famous physics discoveries:

Discovered the law that the period of a pendulum depends on the length of the string, and not on the weight on it. He is said to have discovered this while watching a pendulum in a cathedral, and using his pulse for a timer.

Famous story (probably apocryphal): he dropped a heavy and a light object from the Leaning Tower, in order to prove to his students that rate of fall was independent of weight, refuting Aristotle.

Studied motion. Discovered parabolic path of projectiles.

Astronomy:

Accepted Copernican system.

Built a telescope of 20x magnification. Discovered: craters on the moon, the phases of Venus, & 4 satellites of Jupiter.

The Copernican system had been pronounced heresy in 1616.

Nevertheless, in 1632, he published his Dialogue on the Two Chief World Systems. In it, he defended the Copernican system. Despite its approval by church censors, he was called to Rome to be tried for heresy (1633). He recanted, and was sentenced only to house arrest for the rest of his life.

Somehow, he went ahead and wrote another book, refuting Aristotelian physics, the Dialogues on Two New Sciences.

Died in 1642, the same year Newton was born.

The church forgave him in 1992.

V. Isaac Newton

Dec. 25, 1642 - 1727. Possibly the greatest scientist in history.

Discoveries/studies:

The 'method of fluxions' (differential calculus).

Studied light & colors.

The laws of motion.

The theory of gravity.

The binomial theorem.

Spent his later life studying theology.

More about Newton's biggest discoveries:

Study of the moon's orbit. Assumed there was an inverse square law of gravitation. Used this to argue that the moon is held in its orbit by the same force as terrestrial gravity.

In the Principia Mathematica (1687):

Newton's definitions:

There are 8 definitions:

1. Quantity of matter is a measure of matter that arises from its density and volume jointly.

2. Quantity of motion is a measure of motion that arises from the velocity and the quantity of matter jointly.

+ 6 more.

Laws of motion:

1. Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed.

2. A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.

3. To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction.

Theory of gravity: each particle of matter attracts every other particle. Attraction is proportional to mass, inversely proportional to distance squared. Newton proved results from this:

The gravitational force produced by a spherical body is as if the mass were concentrated at the center.

The gravitational force would produce an elliptical orbit.

It would also produce an orbit in which the orbiting object swept out equal areas in equal times.

The parallelogram law for the composition of forces.

Newton used geometrical methods, rather than fluxions, to avoid controversy about fluxions.

Didn't know how gravity worked, but he rejected 'action at a distance.'

Calculus:

Fluxions & fluents. Fluents are changing quantities; fluxions are their rates of change. Newton dealt with 2 kinds of problems:

"The relation of the fluents being given, to find the relation of their fluxions." (In modern terms: given y as a function of x, to find dy/dx.)

Given the relation of the fluxions, to find the relation of the fluents. (In modern terms: given dy/dx, to find y as a function of x.)

Newton was mainly concerned with motion and change over time, so he considered quantities that are mathematically related as changing over time.

Newton discovered that integration was the inverse operation of differentiation (a.k.a. 'the fundamental theorem of calculus')

Makes it possible to determine velocity function from acceleration

Newton's influence:

Came to be accepted first in Britain, then in the rest of Europe. France held out for several decades, in deference to Descartes.

About Newton's life:

Tried to avoid controversy; avoided publishing

Modest about his accomplishments:

"I do not know what I may appear to the world; but to myself I seem to have been only like a boy, playing on the sea-shore, and diverting myself, in now and then finding a smoother pebble, or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me."

--I. Newton

Anti-social. Not very generous, as shown by his controversy with Leibniz.

Was completely focused on scientific work.

Generally a genius. Known for solving difficult problems posed by other scientists.