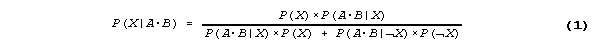
In The Structure of Empirical Knowledge, Laurence BonJour argues that coherence among a set of empirical beliefs can provide justification for those beliefs, in the sense of rendering them likely to be true. He also repudiates all forms of foundationalism for empirical beliefs, including what he calls "weak foundationalism" (the weakest form of foundationalism he can find). In the following, I will argue that coherence cannot provide any justification for our beliefs in the manner BonJour suggests unless some form of foundational justification is assumed. In other words, the argument that BonJour gives in favor of the thesis that coherence provides a kind of justification succeeds if and only if some beliefs have (at least weak) foundational justification.
1. The nature of observation:
According to BonJour, when we make observations, what happens is that we find ourselves spontaneously believing certain very detailed propositions, in the absence of any process of inference nor any exercise of volition or deliberation on our part. For example, I might find myself spontaneously believing that there is a book of a certain size, with a certain shade of red on the cover, and so on, sitting on a desk of a certain size, shape, and color in front of me, etc.(1) BonJour calls these beliefs "cognitively spontaneous beliefs," and they are the heart of his account of observation.
BonJour stresses that these cognitively spontaneous beliefs are not to be construed as foundational, for although they are initially acquired without the exercise of inference, they are not justified unless and until we find reasons for them. If we do not have any reasons (distinct from the beliefs themselves) for thinking our cognitively spontaneous beliefs are likely to be true, then although we may continue to hold them, we won't be epistemically justified in holding them.
2. The argument for coherence justification:
BonJour argues that if our system of beliefs can incorporate a wide range of these cognitively spontaneous beliefs and remain coherent over time, then there is reason to think that our cognitively spontaneous beliefs are generally caused by the sorts of facts that would make them true, and that our belief system in general is largely accurate. The essential reason for this is that on the assumption that our cognitively spontaneous beliefs don't reflect reality, it is very unlikely that they would happen to fit together into a highly coherent picture.
BonJour refers with approval to an instructive example from C.I. Lewis. Suppose that we are interviewing a number of unreliable witnesses. Each witness, we think, is quite likely to lie or misreport. However, suppose we find that all or nearly all of the witnesses tell us the same story. Assuming that the witnesses aren't collaborating, this circumstance makes it highly probable that the story is correct, because if the witnesses were fabricating their stories (and not in communication with each other), it is highly improbable that they would have all happened to agree.(2) Thus, even if each witness has only a very low degree of credibility individually, two or three witnesses' testimony can combine to provide a very high probability of the truth of the story. Similarly, BonJour believes, even if our cognitively spontaneous (observation) beliefs don't have any independent (foundational) justification, the mutual agreement of a large number of them on the same general 'story' can provide adequate justification for the truth of that story.
3. On foundationalism:
BonJour distinguishes three varieties of foundationalism:
(a) Strong foundationalism holds that there are certain basic beliefs that do not depend on inference for their justification, and that the basic beliefs are absolutely certain, or indubitable, etc.
(b) Moderate foundationalism holds that there are basic beliefs that possess a degree of justification independent of their support by other beliefs, that this degree of justification is sufficient for knowledge, but that it does not amount to absolute certainty.
(c) Finally, weak foundationalism holds that the basic beliefs only possess a small degree of non-inferential justification which is insufficient by itself for knowledge, and that we must rely on coherence to amplify our justification up to the level where it would be sufficient for knowledge.
BonJour makes it clear that he wishes to repudiate all forms of foundationalism, including weak foundationalism. In the above argument for coherence justification, we are not to suppose the conclusion is merely that coherence can amplify the level of justification that our observation beliefs start out with; rather, BonJour holds, our observation beliefs start out with no initial degree of justification whatever, and coherence alone provides justification for them:
[Lewis'] example shows quite convincingly that no antecedent degree of warrant or credibility is required. For as long as we are confident that the reports of the various witnesses are genuinely independent of each other, a high enough degree of coherence among them will eventually dictate the hypothesis of truth telling.... And by the same token, so long as apparently cognitively spontaneous beliefs are genuinely independent of each other, their agreement will eventually generate credibility, without the need for any initial degree of warrant.(3)
It is this claim that I aim to refute below: if the witnesses lack any degree of independent credibility, then their mutual agreement will never generate any credibility for their story; and if our cognitively spontaneous beliefs do not possess any degree of foundational justification, then no amount of coherence will ever generate any justification for them either.
BonJour's argument for coherence justification is straightforwardly probabilistic. The natural way to test both Lewis' claim about his own case and BonJour's claims about the case is to specify the assumptions of the case (sufficiently to generate the relevant set of probabilities) and then calculate the relevant prior and conditional probabilities.
For the sake of simplicity, let us suppose that there are two witnesses, Alice and Bert, and that they are reporting on the value of a certain variable, x. x can take on a number of different values -- suppose that there are n possible values that x can assume, and that one of these possible values is x = 2. Assume that each witness is equally credible and that Alice's level of credibility is such that the probability that Alice will report the value of x correctly is r. Now let "X", "A", and "B" stand for the following propositions:
X = The value of x is 2.
A = Alice reports that the value of x is 2.
B = Bert reports that the value of x is 2.
Now, the claim that the concurrence of the two witnesses' testimony confirms that what they attest to is true amounts at least to this: that the probability of X given A and B is higher than the probability of X. What we need now is a general determination of P(X|A&B). We make the following assumptions:
(1) The probability that Alice reports the value of x correctly = the probability that Bert reports correctly = r. (As discussed above.)
(2) There are n possible values of x, each equally likely to be the actual value.
(3) If Alice or Bert reports incorrectly then they select randomly from the n - 1 incorrect values which to report.
(4) Alice's and Bert's answers are entirely independent of each other. (As stipulated by Lewis and BonJour.)
(5) The chances of Alice or Bert reporting incorrectly are independent of what the true value of x is. (Assumed for the sake of simplicity.)
We now set out to calculate P(X|A&B) in terms of n and r. From Bayes' Theorem,
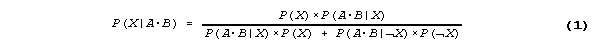
We next determine each of the values on the right hand side of Eq. 1. From assumption (2),
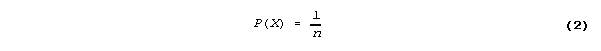
So
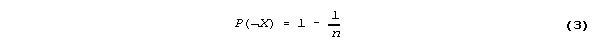
Also,
![]()
whence, since A and B are independent (assumption 2; we may assume they are probabilistically independent relative to X), we get
![]()
From assumptions (1) and (5), we know that P(A|X) = P(B|X) = r, so
![]()
Next,
![]()
Probabilistic independence again dictates that this is equivalent to
![]()
and symmetry considerations dictate that P(A|¬X) = P(B|¬X), since Alice and Bert are equally reliable (or unreliable) and we have given no different information about either of them than we have about the other. Therefore,
![]()
Now, given that the value of x is something other than 2, Alice has a probability of 1 - r of reporting incorrectly (assumptions (1) & (5)). Assuming Alice does report incorrectly, then, we have said, she selects randomly from the n - 1 incorrect values of x to report. Since 2 is one of those values, there is a chance of 1 in n - 1 that Alice would report x = 2. Therefore,
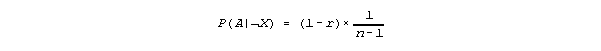
and plugging this into the previous equation,
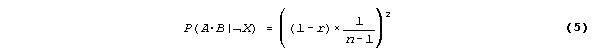
Finally, plugging equations 2, 3, 4, and 5 into Eq. 1, we obtain,
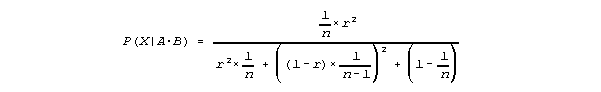
which thankfully simplifies to the following equation:
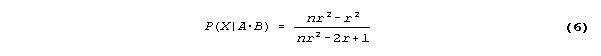
Now, equation 6 is interesting because it exhibits the likelihood
that X is true given that both witnesses have attested that X is true as
a function of two variables: first, the degree of reliability, r, of the
witnesses, and second, the number, n, of possible values of x. This
enables us to vary assumptions about r and n and see what happens to the
probability we're interested in. It also enables us to test both Lewis'
and BonJour's assertions about the hypothetical example in question.
We examine Lewis' claim first. Lewis' fairly modest claim seems to have been just this: that you can get a high degree of confirmation as a result of the agreement of the witnesses even when each witness has only a low degree of credibility considered by himself. As an interpretation of low credibility, let's suppose that Alice and Bert each only tell the truth half of the time. And let's suppose that x has ten possible values. The values of x could be any of a number of things, of course -- possible colors of a car that they claim to have seen; possible last digits in an address; etc. Plugging the values n = 10 and r = 1/2 into equation (6) gives the result (omitting the arithmetic),
![]()
Since the antecedent probability of X would have been .1, this result of
a 90% probability after Alice and Bert both attest that X is fairly
impressive. It looks as if Lewis is correct, which, for precisely the
reason he gave, is not terribly surprising: if X were not the case, it
would be very unlikely that A and B would both happen agree that X.
But this logic simply does not apply in the sort of case BonJour would envision: that is, if there really is no antecedent reason for expecting either of the witnesses to get things right, then the likelihood of the witnesses both reporting X given that X was the right answer would be no better than the likelihood of their both reporting X given that X was one of the wrong answers.
To make the issue more precise, we must formulate BonJour's claim in terms of a probability relation. BonJour says that even if neither witness has any credibility at all, enough coherence will eventually render a belief in X justified. What is the relevant notion of 'credibility'? The interest of the example, of course, is for the analogy that can be drawn to observational beliefs and the degree of initial credibility that a foundationalist would attribute to such beliefs. Now, the natural interpretation of the claim, made by the weak foundationalist, that a given cognitively spontaneous belief carries with it some (possibly very weak) degree of prima facie justification is this: my having a cognitively spontaneous belief that H raises the probability of H. That is, the probability of H given that I have the cognitively spontaneous belief that H is greater than the probability of H. Likewise, in the case of the two witnesses, the statement that Alice has some degree of initial credibility amounts to this: when Alice says that X, the probability of X goes up.
Given this interpretation, we have a well-defined probabilistic question: if we let r be sufficiently low so that P(X|A) = P(X) (i.e. Alice has no credibility), can we still have P(X|A&B) > P(X)? Notice that the only way Alice's testimony will fail by itself to raise the probability of X is if Alice's likelihood of being correct is no better than chance -- that is, if r = 1/n.
In other words: we must set P(X|A) = P(X). P(X) = 1/n. P(X|A) is equal to the probability that Alice is correct given that Alice asserts that x = 2. This is the same as the probability of her being correct if she reports any other value of x, which = r. So we must set r = 1/n. Plugging this into Eq. 6, we get
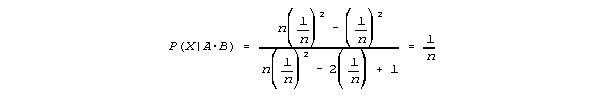
which is exactly the same as the antecedent probability of X, P(X).
Thus, we see that if X receives no confirmation at all from either A or
B individually, then X receives no confirmation at all from A and
B
together. If neither witness has any independent credibility, then the
correspondence of the two witnesses' testimony provides no reason at all
for thinking that what they report is true, and this holds regardless of
how many different stories they could have told -- that is, no matter what
the value of n is, the probability that the witnesses' story is true will
remain equal to 1/n.
This result is, intuitively, not very surprising either. It is, indeed, highly counter-intuitive that one can manufacture confirmation for a hypothesis merely by combining a sufficient number of pieces of evidence that are, individually, completely irrelevant to the hypothesis. And what is perhaps the central anti-coherentist intuition is closely related: one cannot obtain justification for a proposition merely through its agreement with a sufficient number of completely unjustified other propositions.
So where did BonJour's reasoning go wrong? After all, isn't it true that the concurrence of the witnesses' testimony constitutes a surprising coincidence, which requires some explanation? Well, surprising it may be, but the problem is just that under the assumption that the witnesses each have zero independent credibility, the hypothesis that the story they give is the truth is not an explanation of the coincidence. If there is no antecedent presumption that the witnesses are more likely to report the true value of x than to report any other value, the hypothesis that x = 2 is no sort of explanation of the fact of coincidence, since it would not render it any more likely that the witnesses would report that x = 2 (i.e., P(A&B|X) is no greater than P(A&B|¬X)). You might just as well propose the hypothesis that X is false as an explanation of why both witnesses agree that X -- for that would make it just as likely that they would both assert X.
Perhaps it would be said that I'm taking an overly simplified view of explanation -- as if A's explaining B just amounts to A's raising the probability of B. It might be claimed that to explain something is, rather, to cite a causal mechanism, or perhaps that to explain a collection of phenomena is to give a theory that unifies them in a relatively simple way. My response to this is that while such enriched notions of explanation may well be correct, they will not suit BonJour's purposes here. The task that BonJour undertakes, which the argument under discussion is supposed to serve, is to provide an a priori argument for the conclusion that a belief that belongs to a coherent set of beliefs is likely to be true. He would have done this if he could argue that the truth of a certain set of propositions 'explains' why we believe them in the sense of rendering it much more probable that we would believe them (for if H raises the probability of E, then E raises the probability of H, according to Bayes' Theorem). But if that isn't what he's claiming, then the issue of explanation seems to have nothing to do with the probabilistic argument.
Our first conclusion is that weak foundationalism should be taken seriously as an epistemological position. BonJour questions the plausibility of weak foundationalism:
The basic idea is that an initially low degree of justification can somehow be magnified or amplified by coherence, to a degree adequate for knowledge. But how is this magnification or amplification supposed to work? How can coherence, not itself an independent source of justification on a foundationalist view, justify the rejection of some initially credible beliefs and enhance the justification of others.(4)
We have seen the answers to these questions above. In the Lewisian example, we saw that even if P(X|A) is only 1/2, the justification for X reaches 90% with corroboration from a single additional witness. The coherence-amplification effect would obviously be even more pronounced if we assumed a larger range of values for x -- which, not incidentally, would be more typical of real examples (what's the number of distinguishable things I could be visually perceiving at the moment?) -- and corroboration from a larger number of witnesses. The amplification occurs precisely for the reason Lewis states. As long as the truth of X makes it somewhat more likely that each source reports X (in terms of the example, as long as r > 1/n), repeated mutual corroboration will strongly favor the hypothesis of truth. We saw that this does not imply that coherence is an independent source of justification, and that in fact the amplificatory effect of coherence is parasitic on the initial foundational justification. Without that there would be, so to speak, nothing to amplify.
Our second conclusion is that the coherence theory of justification has been seriously undermined. The thrust of BonJour's severe criticisms of foundationalism in The Structure of Empirical Knowledge is this: any theory of justification must explain why the beliefs it identifies as "justified" are likely to be true, and we have no satisfactory explanation of why foundational beliefs are likely to be true. Furthermore, BonJour considers the most fundamental objection to coherentism to be the objection that there's no apparent connection between having an internally coherent belief system and having true beliefs. His bid to show that coherent beliefs are likely to be true is thus the cornerstone of BonJour's theory. The probabilistic argument that we've considered is the sole argument he provides for this crucial point, so the failure of that leaves us with no reason to accept the coherence theory of justification.(5)
1. The Structure of Empirical Knowledge (Cambridge: Harvard University Press, 1985), p. 117.
2. C.I. Lewis, An Analysis of Knowledge and Valuation (La Salle, Ill: Open Court, 1962), p. 346. Discussed in BonJour, pp. 147-8.
3. BonJour, p. 148.
4. p. 29.
5. I would like to thank Barry Loewer and Mike Hardy for their comments on the manuscript and for checking my math.